Next |
Prev |
Up |
Top
|
REALSIMPLE Top
One-Zero String Damping Filter
The original EKS string-damping filter replaced the two-point average
of the KS digitar algorithm by a weighted two-point average
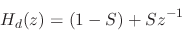 |
(2) |
where ![$S\in[0,1]$](img37.png) is called the ``stretching factor,'' and it adjusts
the relative decay-rate for high versus low frequencies in the string.
This filter goes in the string feedback loop, as shown
in Fig.4 above. At
is called the ``stretching factor,'' and it adjusts
the relative decay-rate for high versus low frequencies in the string.
This filter goes in the string feedback loop, as shown
in Fig.4 above. At 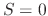 or
or  , the decay time is
``stretched infinitely'' (no decay), while fastest decay is obtained
when
, the decay time is
``stretched infinitely'' (no decay), while fastest decay is obtained
when 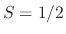 , where it reduces to the KS digitar damping filter. The
decay-time is always infinity for dc, and higher frequencies decay
faster than lower frequencies when
, where it reduces to the KS digitar damping filter. The
decay-time is always infinity for dc, and higher frequencies decay
faster than lower frequencies when 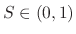 .
.
To control the overall decay rate, another (frequency-independent)
gain multiplier 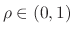 was introduced to give the loop filter
was introduced to give the loop filter
Since this filter is applied once per period 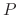 at the fundamental
frequency, an attenuation by the factor
at the fundamental
frequency, an attenuation by the factor
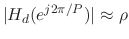 occurs once each
occurs once each 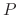 samples.
Setting
samples.
Setting 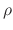 to achieve a decay of
to achieve a decay of 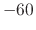 dB in
dB in 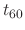 seconds
is obtained by solving
seconds
is obtained by solving
In Faust, we can calculate 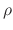 from the desired decay-time in seconds
as follows:
from the desired decay-time in seconds
as follows:
t60 = hslider("decaytime_T60", 4, 0, 10, 0.01); // seconds
rho = pow(0.001,1.0/(freq*t60));
where freq is the fundamental frequency (computed from the
MIDI key number in the example of Fig.9).
The following Faust code implements the original EKS damping filter in
terms of a ``brightness'' parameter 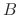 between 0 and 1:
between 0 and 1:
B = hslider("brightness", 0.5, 0, 1, 0.01); // 0-1
b1 = 0.5*B; b0 = 1.0-b1; // S and 1-S
dampingfilter1(x) = rho * (b0 * x + b1 * x');
Relating to Eq. (2), we have the relation
(2), we have the relation 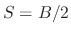 .
.
Next |
Prev |
Up |
Top
|
REALSIMPLE Top
Download faust_strings.pdf
![]() was introduced to give the loop filter
was introduced to give the loop filter
![]() between 0 and 1:
between 0 and 1: