Definition: A function
Definition: A function ![]() is said to be of order
is said to be of order
![]() if
there exist
if
there exist ![]() and some positive constant
and some positive constant ![]() such
that
such
that
![]() for all
for all
![]() .
.
Theorem: (Riemann Lemma):
If the derivatives up to order ![]() of a function
of a function ![]() exist and are
of bounded variation, then its Fourier Transform
exist and are
of bounded variation, then its Fourier Transform ![]() is
asymptotically of order
is
asymptotically of order
![]() , i.e.,
, i.e.,
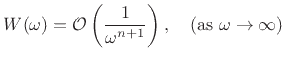 |
(3.42) |
Proof: See §B.18.