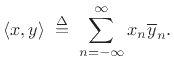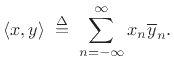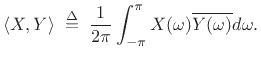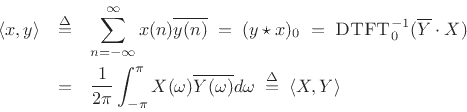Power Theorem for the DTFT

The inner product of two signals may be defined in the time domain by [264]

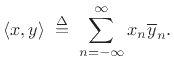$$\left<x,y\right> \isdefs \sum_{n=-\infty}^{\infty} x_n\overline{y}_n.$$ (3.25)

The inner product of two spectra may be defined as

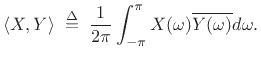$$\left<X,Y\right> \isdefs \frac{1}{2\pi}\int_{-\pi}^\pi X(\omega)\overline{Y(\omega)} d\omega.$$ (3.26)

Note that the frequency-domain inner product includes a normalization factor while the time-domain definition does not.

Using inner-product notation, the power theorem (or Parseval's theorem [202]) for DTFTs can be stated as follows:

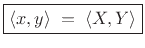$$\zbox {\left<x,y\right> \eqsp \left<X,Y\right>}$$ (3.27)

That is, the inner product of two signals in the time domain equals the inner product of their respective spectra (a complex scalar in general).

When we consider the inner product of a signal with itself, we have the special case known as the energy theorem (or Rayleigh's energy theorem):

$$\Vert x \Vert^2 \eqsp \left<x,x\right> \eqsp \left<X,X\right> \eqsp \Vert X \Vert^2$$ (3.28)

where 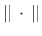$\Vert\,\cdot\,\Vert$ denotes the 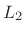$\ensuremath{L_2}$ norm induced by the inner product. It is always real.

Proof: Using the previous correlation theorem:

$$\begin{eqnarray*} \left<x,y\right> &\isdef & \sum_{n=-\infty}^{\infty} x(n)\overline{y(n)} \eqsp (y\star x)_0 \eqsp \hbox{\sc DTFT}_0^{-1}(\overline{Y}\cdot X) \\ &=& \frac{1}{2\pi} \int_{-\pi}^{\pi} X(\omega)\overline{Y(\omega)} d\omega \isdefs \left<X,Y\right> \end{eqnarray*}$$