Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Above, we used the Hilbert transform to find the imaginary part of an
analytic signal from its real part. A closely related application of
the Hilbert transform is constructing a minimum phase
[263] frequency response from an amplitude response.
Let 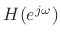 denote a desired complex, minimum-phase frequency response
in the digital domain (
denote a desired complex, minimum-phase frequency response
in the digital domain (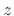 plane):
plane):
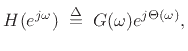 |
(5.23) |
and suppose we have only the amplitude response
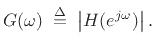 |
(5.24) |
Then the phase response
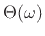 can be computed as the
Hilbert transform of
can be computed as the
Hilbert transform of
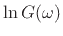 . This can be seen by inspecting
the log frequency response:
. This can be seen by inspecting
the log frequency response:
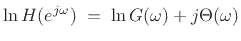 |
(5.25) |
If 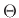 is computed from
is computed from 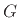 by the Hilbert transform, then
by the Hilbert transform, then
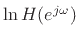 is an ``analytic signal'' in the frequency domain.
Therefore, it has no ``negative times,'' i.e., it is causal. The time
domain signal corresponding to a log spectrum is called the
cepstrum [263]. It is reviewed in the next section
that a frequency response is minimum phase if and only if the
corresponding cepstrum is causal [198, Ch. 10],
[263, Ch. 11].
is an ``analytic signal'' in the frequency domain.
Therefore, it has no ``negative times,'' i.e., it is causal. The time
domain signal corresponding to a log spectrum is called the
cepstrum [263]. It is reviewed in the next section
that a frequency response is minimum phase if and only if the
corresponding cepstrum is causal [198, Ch. 10],
[263, Ch. 11].
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() denote a desired complex, minimum-phase frequency response
in the digital domain (
denote a desired complex, minimum-phase frequency response
in the digital domain (![]() plane):
plane):