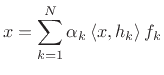Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Geometric Signal Theory
In general, signals can be expanded as a linear combination
of orthonormal basis signals 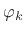 [264]. In the
discrete-time case, this can be expressed as
[264]. In the
discrete-time case, this can be expressed as
where the coefficient of projection of  onto
onto 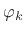 is given by
is given by
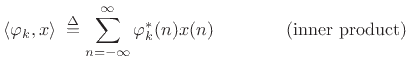 |
(12.105) |
and the basis signals are orthonormal:
 |
(12.106) |
The signal expansion (11.104) can be interpreted geometrically
as a sum of orthogonal projections of 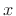 onto
onto
 , as
illustrated for 2D in Fig.11.30.
, as
illustrated for 2D in Fig.11.30.
A set of signals
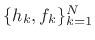 is said to be
a biorthogonal basis set if any signal
is said to be
a biorthogonal basis set if any signal 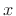 can be represented
as
can be represented
as
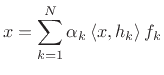 |
(12.107) |
where 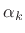 is some normalizing scalar dependent only on
is some normalizing scalar dependent only on 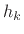 and/or
and/or 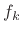 . Thus, in a biorthogonal system, we project onto the
signals
. Thus, in a biorthogonal system, we project onto the
signals 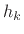 and resynthesize in terms of the basis
and resynthesize in terms of the basis 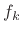 .
.
The following examples illustrate the Hilbert space point of view for
various familiar cases of the Fourier transform and STFT. A more
detailed introduction appears in Book I [264].
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() [264]. In the
discrete-time case, this can be expressed as
[264]. In the
discrete-time case, this can be expressed as
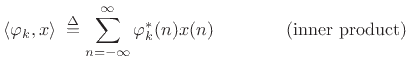

![]() is said to be
a biorthogonal basis set if any signal
is said to be
a biorthogonal basis set if any signal ![]() can be represented
as
can be represented
as