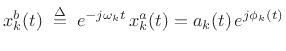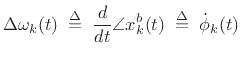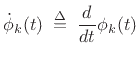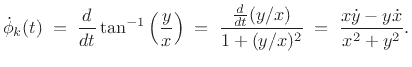Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
It is convenient in practice to work with instantaneous
frequency deviation instead of phase:
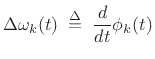 |
(G.9) |
Since the 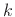 th channel of an
th channel of an 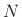 -channel uniform filter-bank has
nominal bandwidth given by
-channel uniform filter-bank has
nominal bandwidth given by 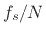 , the frequency deviation usually
does not exceed
, the frequency deviation usually
does not exceed
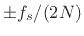 .
.
Note that 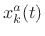 is a narrow-band signal centered about the channel
frequency
is a narrow-band signal centered about the channel
frequency 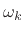 . As detailed in Chapter 9, it is typical
to heterodyne the channel signals to ``base band'' by shifting
the input spectrum by
. As detailed in Chapter 9, it is typical
to heterodyne the channel signals to ``base band'' by shifting
the input spectrum by 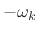 so that the channel bandwidth is
centered about frequency zero (dc). This may be expressed by
modulating the analytic signal by
so that the channel bandwidth is
centered about frequency zero (dc). This may be expressed by
modulating the analytic signal by
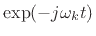 to get
to get
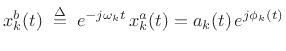 |
(G.10) |
The `b' superscript here stands for ``baseband,'' i.e., the
channel-filter frequency-response is centered about dc. Working at
baseband, we may compute the frequency deviation as simply the
time-derivative of the instantaneous phase of the analytic signal:
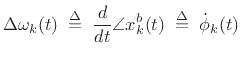 |
(G.11) |
where
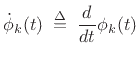 |
(G.12) |
denotes the time derivative of 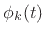 . For notational
simplicity, let
. For notational
simplicity, let
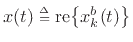 and
and
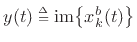 . Then we have
. Then we have
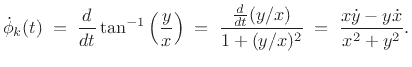 |
(G.13) |
For discrete time, we replace 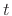 by
by 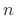 to obtain [186]
to obtain [186]
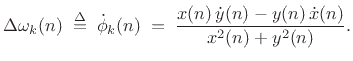 |
(G.14) |
Initially, the sliding FFT was used (hop size  in the
notation of Chapters 8 and 9). Larger hop sizes can result in phase
ambiguities, i.e., it can be ambiguous exactly how many cycles of a
quasi-sinusoidal component occurred during the hop within a given
channel, especially for high-frequency channels. In many
applications, this is not a serious problem, as it is only necessary
to recreate a psychoacoustically equivalent peak trajectory in the
short-time spectrum. For related discussion,
see [300].
in the
notation of Chapters 8 and 9). Larger hop sizes can result in phase
ambiguities, i.e., it can be ambiguous exactly how many cycles of a
quasi-sinusoidal component occurred during the hop within a given
channel, especially for high-frequency channels. In many
applications, this is not a serious problem, as it is only necessary
to recreate a psychoacoustically equivalent peak trajectory in the
short-time spectrum. For related discussion,
see [300].
Using (G.6) and (G.14) to compute the instantaneous
amplitude and frequency for each subband, we obtain data such as shown
qualitatively in Fig.G.12. A matlab algorithm for phase unwrapping
is given in §F.4.1.
![\begin{psfrags}
% latex2html id marker 43455\psfrag{ak} []{ \LARGE$ a_k(t)$\ }\psfrag{wkt} []{ \LARGE$ \Delta\omega_k(t)=\dot{\phi_k}(t) $\ }\psfrag{wk} []{ \LARGE$ 0 $\ }\psfrag{t} []{ \LARGE$ t$\ }\begin{figure}[htbp]
\includegraphics[width=3.5in]{eps/traj}
\caption{Example amplitude envelope (top)
and frequency envelope (bottom).}
\end{figure}
\end{psfrags}](img3025.png)
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
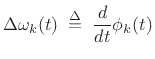
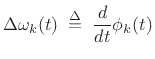
![]() is a narrow-band signal centered about the channel
frequency
is a narrow-band signal centered about the channel
frequency ![]() . As detailed in Chapter 9, it is typical
to heterodyne the channel signals to ``base band'' by shifting
the input spectrum by
. As detailed in Chapter 9, it is typical
to heterodyne the channel signals to ``base band'' by shifting
the input spectrum by ![]() so that the channel bandwidth is
centered about frequency zero (dc). This may be expressed by
modulating the analytic signal by
so that the channel bandwidth is
centered about frequency zero (dc). This may be expressed by
modulating the analytic signal by
![]() to get
to get