Theorem: Let
Theorem: Let ![]() denote a signal with DTFT
denote a signal with DTFT ![]() , and let
, and let
 |
(3.40) |
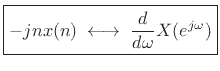
where
Proof:
Using integration by parts, we obtain
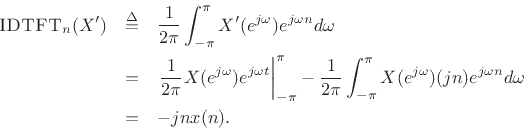
An alternate method of proof is given in §B.3.
Corollary: Perhaps a cleaner statement is as follows:
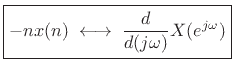
This completes our coverage of selected DTFT theorems. The next section adds some especially useful FT theorems having no precise counterpart in the DTFT (discrete-time) case.