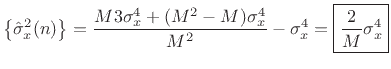Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Consider now the sample variance estimator
 |
(C.33) |
where the mean is assumed to be
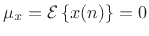 , and
, and
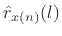 denotes the unbiased sample autocorrelation of
denotes the unbiased sample autocorrelation of 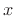 based on the
based on the 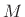 samples leading up to and including time
samples leading up to and including time 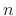 . Since
. Since
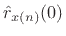 is unbiased,
is unbiased,
![$ {\cal E}\left\{[\hat{\sigma}_x^2(n)]^2\right\} = {\cal E}\left\{\hat{r}_{x(n)}^2(0)\right\} = \sigma_x^2$](img2699.png) .
The variance of this estimator is then given by
.
The variance of this estimator is then given by
where
The autocorrelation of 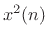 need not be simply related to that of
need not be simply related to that of
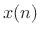 . However, when
. However, when 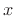 is assumed to be Gaussian white
noise, simple relations do exist. For example, when
is assumed to be Gaussian white
noise, simple relations do exist. For example, when
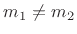 ,
,
 |
(C.34) |
by the independence of  and
and  , and when
, and when  ,
the fourth moment is given by
,
the fourth moment is given by
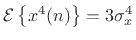 .
More generally, we can simply label the
.
More generally, we can simply label the 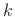 th moment of
th moment of 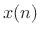 as
as
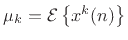 , where
, where 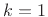 corresponds to the mean,
corresponds to the mean, 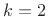 corresponds to the variance (when the mean is zero), etc.
corresponds to the variance (when the mean is zero), etc.
When 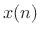 is assumed to be Gaussian white noise, we have
is assumed to be Gaussian white noise, we have
![$\displaystyle {\cal E}\left\{x^2(n-m_1)x^2(n-m_2)\right\} = \left\{\begin{array}{ll} \sigma_x^4, & m_1\ne m_2 \\ [5pt] 3\sigma_x^4, & m_1=m_2 \\ \end{array} \right.$](img2712.png) |
(C.35) |
so that the variance of our estimator for the variance of Gaussian
white noise is
Var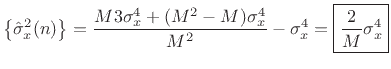 |
(C.36) |
Again we see that the variance of the estimator declines as 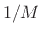 .
.
The same basic analysis as above can be used to estimate the variance
of the sample autocorrelation estimates for each lag, and/or the
variance of the power spectral density estimate at each frequency.
As mentioned above, to obtain a grounding in statistical signal
processing, see references such as
[201,121,95].
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]


![$ {\cal E}\left\{[\hat{\sigma}_x^2(n)]^2\right\} = {\cal E}\left\{\hat{r}_{x(n)}^2(0)\right\} = \sigma_x^2$](img2699.png) .
The variance of this estimator is then given by
.
The variance of this estimator is then given by
![\begin{eqnarray*}
\mbox{Var}\left\{\hat{\sigma}_x^2(n)\right\} &\isdef & {\cal E}\left\{[\hat{\sigma}_x^2(n)-\sigma_x^2]^2\right\}\\
&=& {\cal E}\left\{[\hat{\sigma}_x^2(n)]^2-\sigma_x^4\right\}
\end{eqnarray*}](img2700.png)
![\begin{eqnarray*}
{\cal E}\left\{[\hat{\sigma}_x^2(n)]^2\right\} &=&
\frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_1=0}^{M-1}{\cal E}\left\{x^2(n-m_1)x^2(n-m_2)\right\}\\
&=& \frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_1=0}^{M-1}r_{x^2}(\vert m_1-m_2\vert)
\end{eqnarray*}](img2701.png)
![]() need not be simply related to that of
need not be simply related to that of
![]() . However, when
. However, when ![]() is assumed to be Gaussian white
noise, simple relations do exist. For example, when
is assumed to be Gaussian white
noise, simple relations do exist. For example, when
![]() ,
,
![]() is assumed to be Gaussian white noise, we have
is assumed to be Gaussian white noise, we have
![$\displaystyle {\cal E}\left\{x^2(n-m_1)x^2(n-m_2)\right\} = \left\{\begin{array}{ll} \sigma_x^4, & m_1\ne m_2 \\ [5pt] 3\sigma_x^4, & m_1=m_2 \\ \end{array} \right.$](img2712.png)