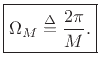Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
We saw in §5.4.1 that our ability to resolve two closely
spaced sinusoids is determined by the main-lobe width of the
window transform we are using. We will now study this relationship in
more detail.
For starters, let's define main-lobe bandwidth very simply (and
somewhat crudely) as the distance between the first
zero-crossings on either side of the main lobe, as shown in
Fig.5.10 for a rectangular-window transform. Let 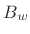 denote this width in Hz. In normalized radian frequency units, as
used in the frequency axis of Fig.5.10,
denote this width in Hz. In normalized radian frequency units, as
used in the frequency axis of Fig.5.10, 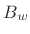 Hz translates to
Hz translates to
 radians per sample, where
radians per sample, where 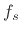 denotes the sampling rate in Hz.
denotes the sampling rate in Hz.
Figure 5.10:
Window transform with main-lobe width marked.
![\includegraphics[width=\twidth]{eps/rectWinMLM}](img962.png) |
For the length-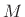 unit-amplitude rectangular window defined in
§3.1, the DTFT is given analytically by
unit-amplitude rectangular window defined in
§3.1, the DTFT is given analytically by
 |
(6.23) |
where 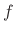 is frequency in Hz, and
is frequency in Hz, and 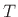 is the sampling interval in
seconds (
is the sampling interval in
seconds (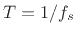 ). The main lobe of the rectangular-window
transform is thus ``two side lobes wide,'' or
). The main lobe of the rectangular-window
transform is thus ``two side lobes wide,'' or
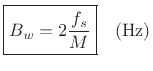 |
(6.24) |
as can be seen in Fig.5.10.
Recall from §3.1.1 that the side-lobe width in a
rectangular-window transform (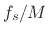 Hz) is given in radians
per sample by
Hz) is given in radians
per sample by
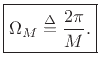 |
(6.25) |
As Fig.5.10 illustrates, the rectangular-window transform
main-lobe width is 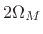 radians per sample (two side-lobe
widths). Table 5.1 lists the main-lobe widths for a
variety of window types (which are defined and discussed further in
Chapter 3).
radians per sample (two side-lobe
widths). Table 5.1 lists the main-lobe widths for a
variety of window types (which are defined and discussed further in
Chapter 3).
Table 5.1:
Main-lobe bandwidth for various windows.
| Window Type |
Main-Lobe Width  (rad/sample)
(rad/sample) |
| Rectangular |
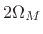
|
| Hamming |
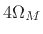
|
| Hann |
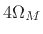
|
| Generalized Hamming |
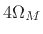
|
| Blackman |
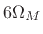
|
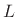 -term Blackman-Harris
-term Blackman-Harris |
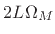
|
| Kaiser |
depends on 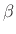
|
| Chebyshev |
depends on ripple spec |
|
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() denote this width in Hz. In normalized radian frequency units, as
used in the frequency axis of Fig.5.10,
denote this width in Hz. In normalized radian frequency units, as
used in the frequency axis of Fig.5.10, ![]() Hz translates to
Hz translates to
![]() radians per sample, where
radians per sample, where ![]() denotes the sampling rate in Hz.
denotes the sampling rate in Hz.
![]() unit-amplitude rectangular window defined in
§3.1, the DTFT is given analytically by
unit-amplitude rectangular window defined in
§3.1, the DTFT is given analytically by
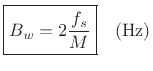
![]() Hz) is given in radians
per sample by
Hz) is given in radians
per sample by