Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
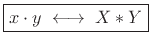
The convolution theorem for Fourier transforms states that
convolution in the time domain equals multiplication in the
frequency domain. The continuous-time
convolution of two signals
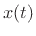 and
and 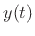 is defined by
is defined by
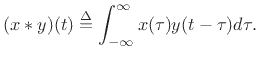 |
(B.15) |
The Fourier transform is then
or,
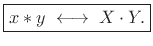 |
(B.16) |
Exercise: Show that
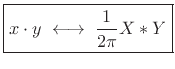 |
(B.17) |
when frequency-domain convolution is defined by
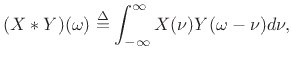 |
(B.18) |
where 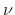 is in radians per second, and that
is in radians per second, and that
 |
(B.19) |
when frequency-domain convolution is defined by
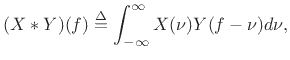 |
(B.20) |
with 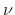 in Hertz.
in Hertz.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() and
and ![]() is defined by
is defined by
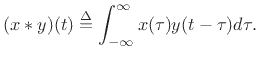
![\begin{eqnarray*}
\hbox{\sc FT}_\omega(x\ast y) &\isdef &
\int_{-\infty}^\infty
\left[\ensuremath{\int_{-\infty}^{\infty}}x(\tau)y(t-\tau)d\tau\right]
e^{-j\omega t}dt\\
&=&
\int_{-\infty}^\infty d\tau\, x(\tau)
\ensuremath{\int_{-\infty}^{\infty}}dt\, y(t-\tau)e^{-j\omega t}\\
&=&
\int_{-\infty}^\infty d\tau\, x(\tau) e^{-j\omega\tau}Y(\omega)
\quad\mbox{(by the \emph{shift theorem})}\\
&=& X(\omega)Y(\omega),
\end{eqnarray*}](img2433.png)
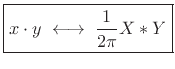
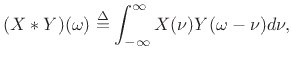
is in radians per second, and that
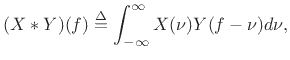
in Hertz.