Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The formula for a general first-order (bilinear) conformal mapping of
functions of a complex variable is conveniently expressed by
[42, page 75]
It can be seen that choosing three specific points and their images
determines the mapping for all
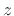 and
and 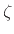 .
.
Bilinear transformations map circles and lines into circles and lines
(lines being viewed as circles passing through the point at infinity).
In digital audio, where both domains are ``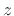 planes,'' we normally
want to map the unit circle to itself, with dc mapping to dc
(
planes,'' we normally
want to map the unit circle to itself, with dc mapping to dc
(
 ) and half the sampling rate mapping to half the
sampling rate (
) and half the sampling rate mapping to half the
sampling rate (
 ). Making these substitutions in
(E.2) leaves us with transformations of the form
). Making these substitutions in
(E.2) leaves us with transformations of the form
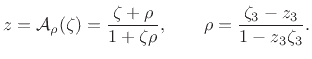 |
(E.1) |
The constant 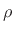 provides one remaining degree of freedom which can
be used to map any particular frequency
provides one remaining degree of freedom which can
be used to map any particular frequency 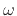 (corresponding to the
point
(corresponding to the
point
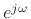 on the unit circle) to a new location
on the unit circle) to a new location
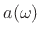 .
All other frequencies will be warped accordingly. Note that
this class of ``circle to circle'' bilinear transformations takes the
form of the transfer function of an allpass filter. We
therefore call it an ``allpass transformation''. The ``allpass
coefficient''
.
All other frequencies will be warped accordingly. Note that
this class of ``circle to circle'' bilinear transformations takes the
form of the transfer function of an allpass filter. We
therefore call it an ``allpass transformation''. The ``allpass
coefficient'' 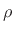 can be written in terms of the frequencies
can be written in terms of the frequencies 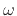 and
and
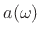 as
as
![$\displaystyle \rho = {\sin\{[a(\omega )-\omega ]/2\} \over \sin\{[a(\omega )+\omega ]/2\} }.$](img2867.png) |
(E.2) |
In this form, it is clear that 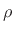 is real, and that the inverse of
is real, and that the inverse of
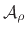 is
is
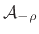 . Also, since
. Also, since
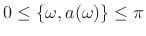 , and
, and
 for an audio warping (where low frequencies must be
``stretched out'' relative to high frequencies), we have
for an audio warping (where low frequencies must be
``stretched out'' relative to high frequencies), we have
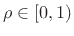 for audio-type mappings from the
for audio-type mappings from the 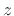 plane to the
plane to the 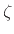 plane.
plane.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
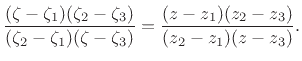
![]() planes,'' we normally
want to map the unit circle to itself, with dc mapping to dc
(
planes,'' we normally
want to map the unit circle to itself, with dc mapping to dc
(
![]() ) and half the sampling rate mapping to half the
sampling rate (
) and half the sampling rate mapping to half the
sampling rate (
![]() ). Making these substitutions in
(E.2) leaves us with transformations of the form
). Making these substitutions in
(E.2) leaves us with transformations of the form
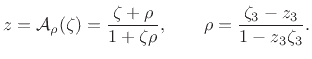
![$\displaystyle \rho = {\sin\{[a(\omega )-\omega ]/2\} \over \sin\{[a(\omega )+\omega ]/2\} }.$](img2867.png)