Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Unloaded Junctions and Alpha Parameters
In the unloaded case, we have 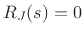 , so there are no dynamics at
the junction, and Eq.(C.99) for the series junction reduces
to
, so there are no dynamics at
the junction, and Eq.(C.99) for the series junction reduces
to
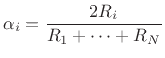 |
(C.126) |
These we call the alpha parameters,
and they are analogous to those
used to characterize ``adaptors'' in wave digital filters (§F.2.2).
For unloaded junctions, the alpha parameters obey
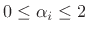 |
(C.127) |
and
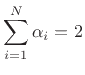 |
(C.128) |
In the unloaded case, the series junction scattering relations are given (in
the time domain) by
The alpha parameters provide an interesting and useful parametrization
of waveguide junctions. They are explicitly the coefficients of the
incoming traveling waves needed to compute junction velocity for a
series junction (or junction force or pressure at a parallel
junction), and losslessness is assured provided only that the alpha
parameters be nonnegative and sum to 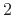 . Having them sum to
something less than
. Having them sum to
something less than 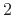 simulates a ``resistive load'' at the
junction.
simulates a ``resistive load'' at the
junction.
Note that in the lossless, equal-impedance case, in which all waveguide
impedances have the same value 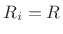 , (C.126) reduces to
, (C.126) reduces to
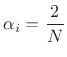 |
(C.131) |
When, furthermore, 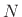 is a power of two, we have that there are
no multiplies in the scattering relations (C.129). This
fact has been used to build multiply-free reverberators and other
structures using digital waveguide meshes
[434,522,399,524].
is a power of two, we have that there are
no multiplies in the scattering relations (C.129). This
fact has been used to build multiply-free reverberators and other
structures using digital waveguide meshes
[434,522,399,524].
An elaborated discussion of 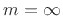 strings intersection at a load is
given in in §9.2.1. Further discussion of the digital waveguide
mesh appears in §C.14.
strings intersection at a load is
given in in §9.2.1. Further discussion of the digital waveguide
mesh appears in §C.14.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() , so there are no dynamics at
the junction, and Eq.(C.99) for the series junction reduces
to
, so there are no dynamics at
the junction, and Eq.(C.99) for the series junction reduces
to
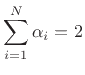
![]() , (C.126) reduces to
, (C.126) reduces to
![]() strings intersection at a load is
given in in §9.2.1. Further discussion of the digital waveguide
mesh appears in §C.14.
strings intersection at a load is
given in in §9.2.1. Further discussion of the digital waveguide
mesh appears in §C.14.