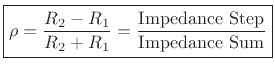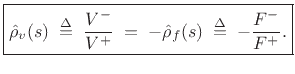Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Simplified Impedance Analysis
The above results are quickly derived from the general
reflection-coefficient for force waves (or voltage waves, pressure
waves, etc.):
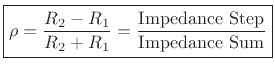 |
(10.17) |
where 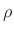 is the reflection coefficient of impedance
is the reflection coefficient of impedance 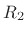 as
``seen'' from impedance
as
``seen'' from impedance 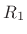 . If a force wave
. If a force wave  traveling along in impedance
traveling along in impedance 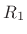 suddenly hits a new impedance
suddenly hits a new impedance
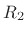 , the wave will split into a reflected wave
, the wave will split into a reflected wave
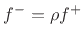 , and a
transmitted wave
, and a
transmitted wave
 . It therefore follows that a velocity
wave
. It therefore follows that a velocity
wave 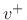 will split into a reflected wave
will split into a reflected wave
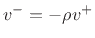 and
transmitted wave
and
transmitted wave
 . This rule is derived in
§C.8.4 (and
implicitly above as well).
. This rule is derived in
§C.8.4 (and
implicitly above as well).
In the mass-string-collision problem, we can immediately write down
the force reflectance of the mass as seen from either string:
That is, waves in the string are traveling through wave impedance
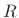 , and when they hit the mass, they are hitting the series
combination of the mass impedance
, and when they hit the mass, they are hitting the series
combination of the mass impedance 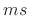 and the wave impedance
and the wave impedance
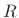 of the string on the other side of the mass. Thus, in terms of
Eq.(9.17) above,
of the string on the other side of the mass. Thus, in terms of
Eq.(9.17) above, 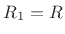 and
and  .
.
Since, by the Ohm's-law relations,
we have that the velocity reflectance is simply
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]