Relation to Stochastic Processes

Property. If a stationary random process $\{x_n\}$ has a rational power spectral density $R\ejo$ corresponding to an autocorrelation function $r(k)={\cal E}\left\{x_nx_{n+k}\right\}$ , then

$$R_+(z)\isdef \frac{r(0)}{ 2} + \sum_{n=1}^\infty r(n)z^{-n}$$

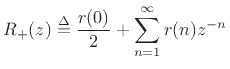
is positive real.

Proof.

By the representation theorem [19, pp. 98-103] there exists an asymptotically stable filter $H(z)=b(z)/a(z)$ which will produce a realization of $\{x_n\}$ when driven by white noise, and we have $R\ejo = H(e^{j\omega})H(e^{-j\omega})$ . We define the analytic continuation of $R\ejo$ by $R(z) = H(z)H(z^{-1})$ . Decomposing $R(z)$ into a sum of causal and anti-causal components gives

$$\begin{eqnarray*} R(z) = \frac{b(z)b(z^{-1})}{ a(z)a(z^{-1})} &=&R_+(z) + R_-(z) \\ &=& \frac{q(z)}{ a(z)}+\frac{q(z^{-1})}{ a(z^{-1})} \end{eqnarray*}$$

where $q(z)$ is found by equating coefficients of like powers of $z$ in

$$b(z)b(z^{-1})=q(z)a(z^{-1}) + a(z)q(z^{-1}).$$

Since the poles of $H(z)$ and $R_+(z)$ are the same, it only remains to be shown that re$\left\{R_+(e^{j\omega})\right\}\geq 0,\;0\leq \omega\leq \pi$ .

Since spectral power is nonnegative, $R\ejo\geq 0$ for all $\omega$ , and so

$$\begin{eqnarray*} R\ejo&\isdef & \sum_{n=-\infty }^\infty r(n)\,e^{j\omega n}\\ &=&r(0) + 2\sum_{n=1}^\infty r(n)\,\cos(\omega n)\\ &=&2\mbox{re}\left\{R_+(e^{j\omega})\right\}\\ &\geq& 0. \end{eqnarray*}$$

$\Box$