Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Figure C.18 shows the more general situation (as compared
to Fig.C.15) of a sinusoidal traveling plane wave
encountering an impedance discontinuity at some arbitrary angle of
incidence, as indicated by the vector wavenumber
 . The
mathematical details of general sinusoidal plane waves in air and
vector wavenumber are reviewed in §B.8.1.
. The
mathematical details of general sinusoidal plane waves in air and
vector wavenumber are reviewed in §B.8.1.
Figure C.18:
Sinusoidal plane wave scattering at an
impedance discontinuity--oblique angle of incidence
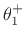 .
.
 |
At the boundary between impedance 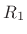 and
and 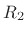 , we have, by
continuity of pressure,
, we have, by
continuity of pressure,
as we will now derive.
Let the impedance change be in the
 plane. Thus, the
impedance is
plane. Thus, the
impedance is 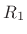 for
for 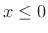 and
and  for
for  . There are three
plane waves to consider:
. There are three
plane waves to consider:
- The incident plane wave with wave vector

- The reflected plane wave with wave vector

- The transmitted plane wave with wave vector
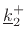
By continuity, the waves must agree on boundary plane:
where
 denotes any vector in the boundary plane. Thus,
at
denotes any vector in the boundary plane. Thus,
at 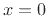 we have
we have
If the incident wave is constant along 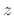 , then
, then
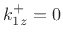 , requiring
, requiring
 , leaving
, leaving
or
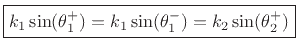 |
(C.56) |
where 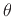 is defined as zero when traveling in the direction of
positive
is defined as zero when traveling in the direction of
positive 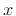 for the incident (
for the incident (
 ) and transmitted (
) and transmitted (
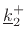 )
wave vector, and along negative
)
wave vector, and along negative 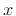 for the reflected
(
for the reflected
(
 ) wave vector (see Fig.C.18).
) wave vector (see Fig.C.18).
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() . The
mathematical details of general sinusoidal plane waves in air and
vector wavenumber are reviewed in §B.8.1.
. The
mathematical details of general sinusoidal plane waves in air and
vector wavenumber are reviewed in §B.8.1.

![]() and
and ![]() , we have, by
continuity of pressure,
, we have, by
continuity of pressure,
![]() plane. Thus, the
impedance is
plane. Thus, the
impedance is ![]() for
for ![]() and
and ![]() for
for ![]() . There are three
plane waves to consider:
. There are three
plane waves to consider: