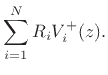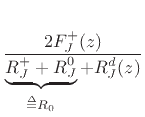Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
In the current situation, computing the junction-velocity 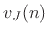 from the incoming waves
from the incoming waves 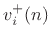 using the parallel biquad expansion
Eq.(C.104) for
using the parallel biquad expansion
Eq.(C.104) for 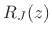 , we split each term
of Eq.(C.102) into its instantaneous and delayed
components [25]:C.12
, we split each term
of Eq.(C.102) into its instantaneous and delayed
components [25]:C.12
so that
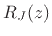 |
 |
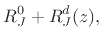 where where |
(C.109) |
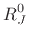 |
 |
 and and |
(C.110) |
 |
 |
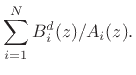 |
(C.111) |
Define
Then Eq.(C.97) can be written
This structure can be realized as shown in Fig.C.30 and derived above.
This form is convenient for encoding in FAUST [471].
Here,  denotes the sum of all incoming wave impedances
denotes the sum of all incoming wave impedances 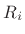 plus
the instantaneous impedance of the load
plus
the instantaneous impedance of the load 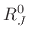 .
.
More directly derived, we can write Eq.(C.97) as
This expression can be taken by inspection to the time domain
in terms of the parallel biquads 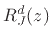 to yield the following difference equation:
to yield the following difference equation:
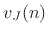 |
 |
![$\displaystyle \frac{1}{R_0} \left[2f_J^+(n) - f_J^d(n)\right],\;$](img4015.png) where where |
(C.119) |
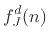 |
 |
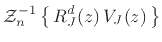 |
(C.120) |
| |
 |
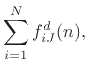 where where |
(C.121) |
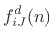 |
 |
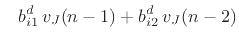 |
|
| |
|
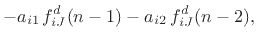 |
(C.122) |
and
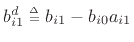 and
and
 ,
as in Eq.(C.108) above.
,
as in Eq.(C.108) above.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() from the incoming waves
from the incoming waves ![]() using the parallel biquad expansion
Eq.(C.104) for
using the parallel biquad expansion
Eq.(C.104) for ![]() , we split each term
of Eq.(C.102) into its instantaneous and delayed
components [25]:C.12
, we split each term
of Eq.(C.102) into its instantaneous and delayed
components [25]:C.12
 and
and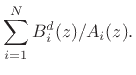
 and
and