Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Let 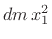 denote the moment of inertia for a rotation axis passing
through the center of mass, and let
denote the moment of inertia for a rotation axis passing
through the center of mass, and let 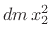 denote
the moment of inertia for a rotation axis parallel to the first
but a distance
denote
the moment of inertia for a rotation axis parallel to the first
but a distance 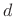 away from it. Then the parallel axis theorem
says that
away from it. Then the parallel axis theorem
says that
where 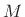 denotes the total mass. Thus, the added inertia due to
displacement by
denotes the total mass. Thus, the added inertia due to
displacement by 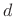 meters away from the centroidal axis is equal to
that of a point mass
meters away from the centroidal axis is equal to
that of a point mass 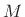 rotating a distance
rotating a distance 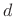 from the
center of rotation.
from the
center of rotation.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() denote the moment of inertia for a rotation axis passing
through the center of mass, and let
denote the moment of inertia for a rotation axis passing
through the center of mass, and let ![]() denote
the moment of inertia for a rotation axis parallel to the first
but a distance
denote
the moment of inertia for a rotation axis parallel to the first
but a distance ![]() away from it. Then the parallel axis theorem
says that
away from it. Then the parallel axis theorem
says that