Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
In many applications, it is possible to realize vast computational savings
in digital waveguide models by commuting losses out of unobserved and
undriven sections of the medium and consolidating them at a minimum number
of points. Because the digital simulation is linear and time invariant
(given constant medium parameters
 ), and because linear,
time-invariant elements commute, the diagram in Fig.C.6 is
exactly equivalent (to within numerical precision) to the previous diagram
in Fig.C.5.
), and because linear,
time-invariant elements commute, the diagram in Fig.C.6 is
exactly equivalent (to within numerical precision) to the previous diagram
in Fig.C.5.
Figure C.6:
Discrete simulation of the ideal, lossy waveguide.
Each per-sample loss factor 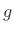 may be ``pushed through'' delay
elements and combined with other loss factors until an input or output
is encountered which inhibits further migration. If further
consolidation is possible on the other side of a branching node, a
loss factor can be pushed through the node by pushing a copy
into each departing branch. If there are other inputs to the
node, the inverse of the loss factor must appear on each of
them. Similar remarks apply to pushing backwards through a node.
may be ``pushed through'' delay
elements and combined with other loss factors until an input or output
is encountered which inhibits further migration. If further
consolidation is possible on the other side of a branching node, a
loss factor can be pushed through the node by pushing a copy
into each departing branch. If there are other inputs to the
node, the inverse of the loss factor must appear on each of
them. Similar remarks apply to pushing backwards through a node.
![\includegraphics[scale=0.9]{eps/flloss}](img3347.png) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() ), and because linear,
time-invariant elements commute, the diagram in Fig.C.6 is
exactly equivalent (to within numerical precision) to the previous diagram
in Fig.C.5.
), and because linear,
time-invariant elements commute, the diagram in Fig.C.6 is
exactly equivalent (to within numerical precision) to the previous diagram
in Fig.C.5.
![\includegraphics[scale=0.9]{eps/flloss}](img3347.png)