Consider a system of ![]() point-masses
point-masses ![]() , each traveling with
vector velocity
, each traveling with
vector velocity
![]() , and not necessarily rigidly attached to
each other. Then the total momentum of the system is
, and not necessarily rigidly attached to
each other. Then the total momentum of the system is
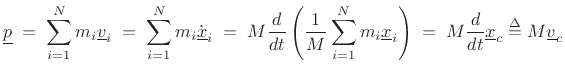
where
Thus, the momentum
![]() of any collection of masses
of any collection of masses ![]() (including rigid bodies) equals the total mass
(including rigid bodies) equals the total mass ![]() times the
velocity of the center-of-mass.
times the
velocity of the center-of-mass.