Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Since the pluck model is linear, the parameters are not
signal-dependent. As a result, when the string and spring separate,
there is a discontinuous change in the reflection and transmission
coefficients. In practice, it is useful to ``feather'' the
switch-over from one model to the next [473]. In
this instance, one appealing choice is to introduce a nonlinear
spring, as is commonly used for piano-hammer models (see
§9.3.2 for details).
Let the nonlinear spring model take the form
where 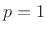 corresponds to a linear spring. The spring constant
linearized about zero displacement
corresponds to a linear spring. The spring constant
linearized about zero displacement 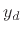 is
is
which, for 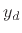 , approaches zero as
, approaches zero as 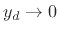 . In other words, the
spring-constant itself goes to zero with its displacement, instead of
remaining a constant. This behavior serves to ``feather'' contact and
release with the string. We see from Eq.(9.23) above
that, as displacement goes to zero, the reflectance approaches a
frequency-independent reflection coefficient
. In other words, the
spring-constant itself goes to zero with its displacement, instead of
remaining a constant. This behavior serves to ``feather'' contact and
release with the string. We see from Eq.(9.23) above
that, as displacement goes to zero, the reflectance approaches a
frequency-independent reflection coefficient
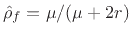 ,
resulting from the damping
,
resulting from the damping 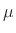 that remains in the spring model. As
a result, there is still a discontinuity when the spring disengages
from the string.
that remains in the spring model. As
a result, there is still a discontinuity when the spring disengages
from the string.
The foregoing suggests a nonlinear tapering of the damping 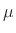 in
addition to the tapering the stiffness
in
addition to the tapering the stiffness 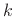 as the spring compression
approaches zero. One natural choice would be
as the spring compression
approaches zero. One natural choice would be
so that 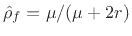 approaches zero at the same rate as
approaches zero at the same rate as 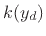 . It
would be interesting to estimate
. It
would be interesting to estimate 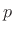 for the spring and damper from
measured data. In the absence of such data,
for the spring and damper from
measured data. In the absence of such data, 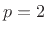 is easy to compute
(requiring a single multiplication). More generally, an interpolated
lookup of
is easy to compute
(requiring a single multiplication). More generally, an interpolated
lookup of 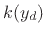 values can be used.
values can be used.
In summary, the engagement and disengagement of the plucking system
can be ``feathered'' by a nonlinear spring and damper in the plectrum
model.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() in
addition to the tapering the stiffness
in
addition to the tapering the stiffness ![]() as the spring compression
approaches zero. One natural choice would be
as the spring compression
approaches zero. One natural choice would be