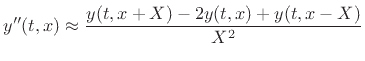
Substituting the FDA into the wave equation gives
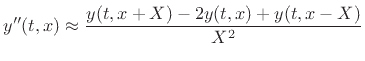
which can be solved to yield the following recursion for the string displacement:
Perhaps surprisingly, it is shown in Appendix E that the above recursion is exact at the sample points in spite of the apparent crudeness of the finite difference approximation [445]. The FDA approach to numerical simulation was used by Pierre Ruiz in his work on vibrating strings [395], and it is still in use today [74,75].
When more terms are added to the wave equation, corresponding to complex
losses and dispersion characteristics, more terms of the form
![]() appear in (C.6). These higher-order terms correspond to
frequency-dependent losses and/or dispersion characteristics in
the FDA. All linear differential equations with constant coefficients give rise to
some linear, time-invariant discrete-time system via the FDA.
A general subclass of the linear, time-invariant case
giving rise to ``filtered waveguides'' is
appear in (C.6). These higher-order terms correspond to
frequency-dependent losses and/or dispersion characteristics in
the FDA. All linear differential equations with constant coefficients give rise to
some linear, time-invariant discrete-time system via the FDA.
A general subclass of the linear, time-invariant case
giving rise to ``filtered waveguides'' is
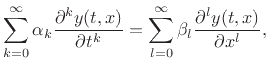 |
(C.7) |
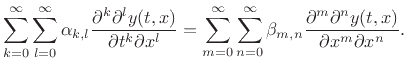 |
(C.8) |
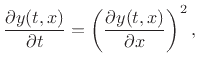 |
(C.9) |
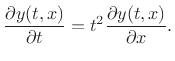 |
(C.10) |