Plotting Complex Sinusoids as Circular Motion

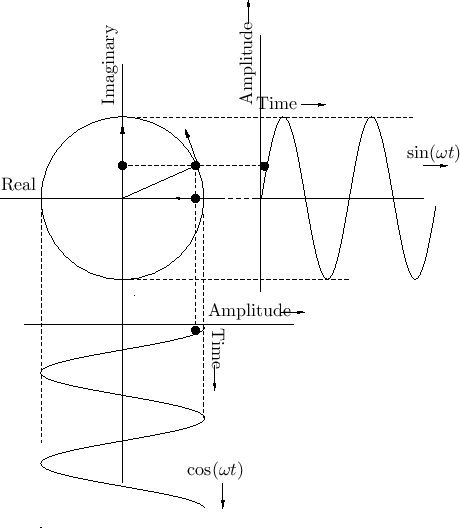
Figure 1.8 shows Euler's relation graphically as it applies to sinusoids. A point traveling with uniform velocity around a circle with radius 1 may be represented by $e^{j\omega t}=e^{j2\pi f t}$ in the complex plane, where $t$ is time and $f$ is the number of revolutions per second. The projection of this motion onto the horizontal (real) axis is $\cos (\omega t)$ , and the projection onto the vertical (imaginary) axis is $\sin (\omega t)$ . For discrete-time circular motion, replace $t$ by $nT$ to get $e^{j\omega nT} = e^{j2\pi (f/f_s) n}$ which may be interpreted as a point which jumps an arc length $2\pi f/f_s$ radians along the circle each sampling instant.

Figure 1.8: Relation of uniform circular motion to sinusoidal motion via Euler's identity $\exp (j\omega t) = \cos (\omega t) + j\sin (\omega t)$ (Eq.(1.8)). The projection of $\exp (j\omega t)$ onto the real axis is $\cos (\omega t)$ , and its projection onto the imaginary axis is $\sin (\omega t)$ .

Figure 1.9: Opposite circular motions add to give real sinusoidal motion, $e^{j\omega t} + e^{-j\omega t} = 2\cos (\omega t)$ .

$\parbox{0.8\textwidth}{% \emph{Euler's identity says that a complex sinusoid corresponds to circular motion in the complex plane, and is the vector sum of two sinusoidal motions.} }$

For circular motion to ensue, the sinusoidal motions must be at the same frequency, one-quarter cycle out of phase, and perpendicular (orthogonal) to each other. (With phase differences other than one-quarter cycle, the motion is generally elliptical.)

The converse of this is also illuminating. Take the usual circular motion $e^{j\omega t}$ which spins counterclockwise along the unit circle as $t$ increases, and add to it a similar but clockwise circular motion $e^{-j\omega t}$ . This is shown in Fig.1.9. Next apply Euler's identity to get

$$\begin{eqnarray*} e^{j\omega t} + e^{-j\omega t} & = & [\cos(\omega t) + j \sin(\omega t)] + [\cos(-\omega t) + j \sin(- \omega t)]\\ & = & \cos(\omega t) + j \sin(\omega t) + \cos(\omega t) - j \sin(\omega t)\\ &=& 2 \cos(\omega t) \end{eqnarray*}$$

Thus,

$\parbox{0.8\textwidth}{% \emph{\emph{Cosine} motion is the vector sum of two circular motions with the same angular speed but opposite direction.}}$

This statement is a graphical or geometric interpretation of Eq.(1.11). A similar derivation (subtracting instead of adding) gives the sine identity Eq.(1.12).

We call $e^{j\omega t}$ a positive-frequency sinusoidal component when $\omega > 0$ , and $e^{-j\omega t}$ is the corresponding negative-frequency component. Note that both sine and cosine signals have equal-amplitude positive- and negative-frequency components (see also [84,53]). This happens to be true of every real signal (i.e., non-complex). To see this, recall that every signal can be represented as a sum of complex sinusoids at various frequencies (its Fourier expansion). For the signal to be real, every positive-frequency complex sinusoid must be summed with a negative-frequency sinusoid of equal amplitude. In other words, any counterclockwise circular motion must be matched by an equal and opposite clockwise circular motion in order that the imaginary parts always cancel to yield a real signal (see Fig.1.9). Thus, a real signal always has a magnitude spectrum which is symmetric about 0 Hz. Fourier symmetries such as this are developed more completely in [84].