Another way to express the allpass condition
![]() is to
write
is to
write
This form generalizes by analytic continuation (see §D.2) to
Definition: The
paraconjugate of a transfer function may be defined as the
analytic continuation of the complex conjugate from the unit circle to
the whole ![]() plane:
plane:
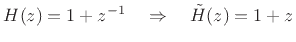
where
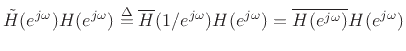
in which the conjugation of
Examples:
We refrain from conjugating ![]() in the definition of the paraconjugate
because
in the definition of the paraconjugate
because
![]() is not analytic in the complex-variables sense.
Instead, we invert
is not analytic in the complex-variables sense.
Instead, we invert ![]() , which is analytic, and which
reduces to complex conjugation on the unit circle.
, which is analytic, and which
reduces to complex conjugation on the unit circle.
The paraconjugate may be used to characterize allpass filters as follows:
Theorem: A causal, stable, filter ![]() is allpass if and only if
is allpass if and only if
Note that this is equivalent to the previous result on the unit circle since
