Impulse Response

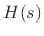
In the same way that the impulse response of a digital filter is given by the inverse z transform of its transfer function, the impulse response of an analog filter is given by the inverse Laplace transform of its transfer function, viz.,

$$h(t) \eqsp {\cal L}_t^{-1}\{H(s)\} \eqsp \frac{1}{\tau}\, e^{-t/\tau} u(t)$$

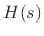
where the scaling by $1/\tau$ gives unity-gain in the passband, and $u(t)$ denotes the Heaviside unit step function

$$u(t) \isdef \left\{\begin{array}{ll} 1, & t\geq 0 \\ [5pt] 0, & t<0. \\ \end{array} \right.$$

This result is most easily checked by taking the Laplace transform of an exponential decay with time-constant $\tau>0$ :

$$\begin{eqnarray*} {\cal L}_s\{e^{-t/\tau}\} &\isdef & \int_0^{\infty}e^{-t/\tau} e^{-st} dt \eqsp \int_0^{\infty}e^{-(s+1/\tau)t} dt\\ &=&\left. \frac{-1}{s+1/\tau} e^{-(s+1/\tau)t} \right\vert _0^\infty\\ &=& \frac{1}{s+1/\tau} = \frac{RC}{RCs+1}. \end{eqnarray*}$$

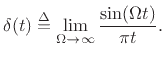
In more complicated situations, any rational $H(s)$ (ratio of polynomials in $s$ ) may be expanded into first-order terms by means of a partial fraction expansion (see §6.8) and each term in the expansion inverted by inspection as above.