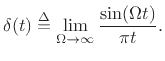The Continuous-Time Impulse

The continuous-time impulse response was derived above as the inverse-Laplace transform of the transfer function. In this section, we look at how the impulse itself must be defined in the continuous-time case.

An impulse in continuous time may be loosely defined as any ``generalized function'' having ``zero width'' and unit area under it. A simple valid definition is

$$\delta(t) \isdef \lim_{\Delta \to 0} \left\{\begin{array}{ll} \frac{1}{\Delta}, & 0\leq t\leq \Delta \\ [5pt] 0, & \hbox{otherwise}. \\ \end{array} \right. \protect$$ (E.5)

More generally, an impulse can be defined as the limit of any pulse shape which maintains unit area and approaches zero width at time 0. As a result, the impulse under every definition has the so-called sifting property under integration,

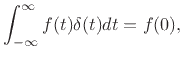$$\int_{-\infty}^\infty f(t) \delta(t) dt = f(0), \protect$$ (E.6)

provided $f(t)$ is continuous at 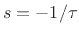$t=0$ . This is often taken as the defining property of an impulse, allowing it to be defined in terms of non-vanishing function limits such as

$$\delta(t) \isdef \lim_{\Omega\to\infty}\frac{\sin(\Omega t)}{\pi t}.$$

An impulse is not a function in the usual sense, so it is called instead a distribution or generalized function [13,44]. (It is still commonly called a ``delta function'', however, despite the misnomer.)