Difference Equation

The difference equation is a formula for computing an output sample at time $n$ based on past and present input samples and past output samples in the time domain.^6.1We may write the general, causal, LTI difference equation as follows:

$$y(n) = b_0 \,x(n) + b_1 \,x(n - 1) + \cdots + b_M \,x(n - M)$$

$$\qquad\quad\; - a_1 \,y(n - 1) - \cdots - a_N \,y(n - N)$$

$$= \sum_{i=0}^M b_i \,x(n-i) - \sum_{j=1}^N a_j \,y(n-j) \protect$$ (6.1)

where $x$ is the input signal, $y$ is the output signal, and the constants $b_i, i = 0, 1, 2, \ldots, M$ , $a_j, j = 1, 2, \ldots, N$ are called the coefficients

As a specific example, the difference equation

$$y(n) = 0.01\, x(n) + 0.002\, x(n - 1) + 0.99\, y(n - 1)$$

specifies a digital filtering operation, and the coefficient sets $(0.01, 0.002)$ and $(0.99)$ fully characterize the filter. In this example, we have $M = N = 1$ .

When the coefficients are real numbers, as in the above example, the filter is said to be real. Otherwise, it may be complex.

Notice that a filter of the form of Eq.(5.1) can use ``past'' output samples (such as $y(n-1)$ ) in the calculation of the ``present'' output $y(n)$ . This use of past output samples is called feedback. Any filter having one or more feedback paths ($N>0$ ) is called recursive. (By the way, the minus signs for the feedback in Eq.(5.1) will be explained when we get to transfer functions in §6.1.)

More specifically, the $b_i$ coefficients are called the feedforward coefficients and the $a_i$ coefficients are called the feedback coefficients.

A filter is said to be recursive if and only if $a_i\neq 0$ for some $i>0$ . Recursive filters are also called infinite-impulse-response (IIR) filters. When there is no feedback ( $a_i=0, \forall i>0$ ), the (finite-order) filter is said to be a nonrecursive or finite-impulse-response (FIR) digital filter.

When used for discrete-time physical modeling, the difference equation may be referred to as an explicit finite difference scheme.^6.2

Showing that a recursive filter is LTI (Chapter 4) is easy by considering its impulse-response representation (discussed in §5.6). For example, the recursive filter

$$\begin{eqnarray*} y(n) &=& x(n) + \frac{1}{2}y(n-1) \\ &=& x(n) + \frac{1}{2}x(n-1) + \frac{1}{4}x(n-2) + \frac{1}{8}x(n-3) + \cdots, \end{eqnarray*}$$

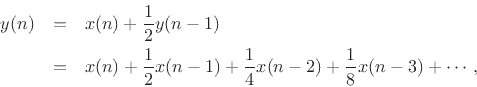
has impulse response $h(m) = 2^{-m}$ , $m=0,1,2,\ldots\,$ . It is now straightforward to apply the analysis of the previous chapter to find that time-invariance, superposition, and the scaling property hold.