Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
From the convolution representation, Eq.(5.5), we have that the output 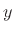 from a linear
time-invariant filter with input
from a linear
time-invariant filter with input 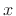 and impulse response
and impulse response 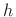 is given
by the convolution of
is given
by the convolution of 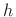 and
and 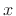 , i.e.,
, i.e.,
 |
(7.3) |
where `` '' means convolution as before. Taking the z transform of
both sides of Eq.(6.3) and applying the convolution theorem from
the preceding section gives
'' means convolution as before. Taking the z transform of
both sides of Eq.(6.3) and applying the convolution theorem from
the preceding section gives
 |
(7.4) |
where H(z) is the z transform of the filter impulse response.
We may divide Eq.(6.4) by 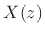 to obtain
to obtain
This shows that, as a direct result of the convolution theorem, the
z transform of an impulse response 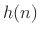 is equal to the transfer
function
is equal to the transfer
function
 of the filter, provided the filter is linear
and time invariant.
of the filter, provided the filter is linear
and time invariant.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() from a linear
time-invariant filter with input
from a linear
time-invariant filter with input ![]() and impulse response
and impulse response ![]() is given
by the convolution of
is given
by the convolution of ![]() and
and ![]() , i.e.,
, i.e.,
