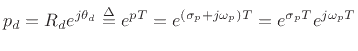Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Consider the continuous-time complex one-pole
resonator with  -plane transfer function
-plane transfer function
where
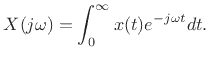 is the Laplace-transform variable, and
is the Laplace-transform variable, and
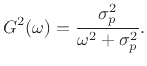 is the single complex pole. The numerator scaling
has been set to
is the single complex pole. The numerator scaling
has been set to 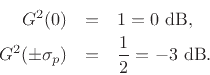 so that the frequency response is normalized to
unity gain at resonance:
so that the frequency response is normalized to
unity gain at resonance:
The amplitude response at all frequencies is given by
Without loss of generality, we may set
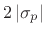 , since changing
, since changing 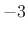 merely translates the amplitude response with respect to
merely translates the amplitude response with respect to 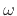 .
(We could alternatively define the translated frequency variable
.
(We could alternatively define the translated frequency variable
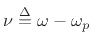 to get the same simplification.) The squared amplitude response is now
to get the same simplification.) The squared amplitude response is now
Note that
This shows that the 3-dB bandwidth of the resonator in radians
per second is
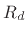 , or twice the absolute value of the real
part of the pole. Denoting the 3-dB bandwidth in Hz by
, or twice the absolute value of the real
part of the pole. Denoting the 3-dB bandwidth in Hz by  , we have
derived the relation
, we have
derived the relation
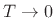 , or
, or
Since a  dB attenuation is the same thing as a power scaling by
dB attenuation is the same thing as a power scaling by
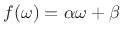 , the 3-dB bandwidth is also called the half-power
bandwidth.
, the 3-dB bandwidth is also called the half-power
bandwidth.
It now remains to ``digitize'' the continuous-time resonator and show
that relation Eq.(8.7) follows. The most natural mapping of the
 plane to the
plane to the 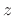 plane is
plane is
where 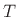 is the sampling period. This mapping follows directly from
sampling the time axis in the Laplace transform to obtain the z transform. It is
also called the impulse invariant transformation [68, pp.
216-219], and for digital poles it is the same as the
matched z transformation [68, pp. 224-226].
Applying the matched z transformation to the pole
is the sampling period. This mapping follows directly from
sampling the time axis in the Laplace transform to obtain the z transform. It is
also called the impulse invariant transformation [68, pp.
216-219], and for digital poles it is the same as the
matched z transformation [68, pp. 224-226].
Applying the matched z transformation to the pole 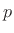 in the
in the  plane gives the digital pole
plane gives the digital pole
from which we identify
and the relation between pole radius  and analog 3-dB bandwidth
and analog 3-dB bandwidth
 (in Hz) is now shown. Since the mapping
(in Hz) is now shown. Since the mapping
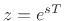 becomes
exact as
becomes
exact as  , we have that
, we have that  is also the 3-dB bandwidth of the
digital resonator in the limit as the sampling rate approaches
infinity. In practice, it is a good approximate relation whenever the
digital pole is close to the unit circle (
is also the 3-dB bandwidth of the
digital resonator in the limit as the sampling rate approaches
infinity. In practice, it is a good approximate relation whenever the
digital pole is close to the unit circle (
 ).
).
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() -plane transfer function
-plane transfer function
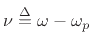
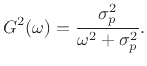 is the single complex pole. The numerator scaling
has been set to
is the single complex pole. The numerator scaling
has been set to 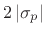
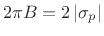
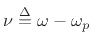 to get the same simplification.) The squared amplitude response is now
to get the same simplification.) The squared amplitude response is now
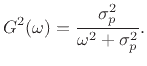
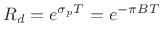
![]() , or twice the absolute value of the real
part of the pole. Denoting the 3-dB bandwidth in Hz by
, or twice the absolute value of the real
part of the pole. Denoting the 3-dB bandwidth in Hz by ![]() , we have
derived the relation
, we have
derived the relation
![]() , or
, or
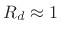
![]() plane to the
plane to the ![]() plane is
plane is