The vector
![]() in a modal representation (Eq.(G.21)) specifies how
the modes are driven by the input. That is, the
in a modal representation (Eq.(G.21)) specifies how
the modes are driven by the input. That is, the ![]() th mode
receives the input signal
th mode
receives the input signal ![]() weighted by
weighted by
![]() . In a computational
model of a drum, for example,
. In a computational
model of a drum, for example,
![]() may be changed corresponding to
different striking locations on the drumhead.
may be changed corresponding to
different striking locations on the drumhead.
The vector
![]() in a modal representation (Eq.(G.21)) specifies how
the modes are to be mixed into the output. In other words,
in a modal representation (Eq.(G.21)) specifies how
the modes are to be mixed into the output. In other words,
![]() specifies how the output signal is to be created as a
linear combination of the mode states:
specifies how the output signal is to be created as a
linear combination of the mode states:
In a computational model of an electric guitar string, for example,
The modal representation is not unique since
![]() and
and
![]() may be scaled in compensating ways to produce the same transfer
function. (The diagonal elements of
may be scaled in compensating ways to produce the same transfer
function. (The diagonal elements of ![]() may also be permuted along
with
may also be permuted along
with
![]() and
and
![]() .) Each element of the state vector
.) Each element of the state vector
![]() holds the state of a single first-order mode of the system.
holds the state of a single first-order mode of the system.
For oscillatory systems, the diagonalized state transition matrix must
contain complex elements. In particular, if mode ![]() is both
oscillatory and undamped (lossless), then an excited
state-variable
is both
oscillatory and undamped (lossless), then an excited
state-variable
![]() will oscillate sinusoidally,
after the input becomes zero, at some frequency
will oscillate sinusoidally,
after the input becomes zero, at some frequency ![]() , where
, where
relates the system eigenvalue
where
In practice, we often prefer to combine complex-conjugate pole-pairs
to form a real, ``block-diagonal'' system; in this case, the
transition matrix ![]() is block-diagonal with two-by-two real matrices
along its diagonal of the form
is block-diagonal with two-by-two real matrices
along its diagonal of the form
![$\displaystyle \mathbf{A}_i = \left[\begin{array}{cc} 2R_iC_i & -R_i^2 \\ [2pt] 1 & 0 \end{array}\right]
$](img2264.png)
where
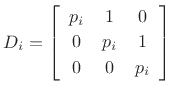 re
re