Inverting the Z Transform

The partial fraction expansion (PFE) provides a simple means for inverting the z transform of rational transfer functions. The PFE provides a sum of first-order terms of the form

$$H_i(z) \eqsp \frac{r_i}{1-p_iz^{-1}}.$$

It is easily verified that such a term is the z transform of

$$h_i(n) \eqsp r_i p_i^n, \quad n=0,1,2,\ldots\,.$$

Thus, the inverse z transform of $H(z)$ is simply

$$h(n) \eqsp \sum_{i=1}^N h_i(n) \eqsp \sum_{i=1}^N r_i p_i^n, \quad n=0,1,2,\ldots\,.$$

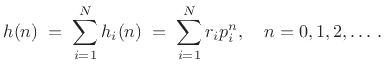
Thus, the impulse response of every strictly proper LTI filter (with distinct poles) can be interpreted as a linear combination of sampled complex exponentials. Recall that a uniformly sampled exponential is the same thing as a geometric sequence. Thus, $h$ is a linear combination of $N$ geometric sequences. The term ratio of the $i$ th geometric sequence is the $i$ th pole, $p_i$ , and the coefficient of the $i$ th sequence is the $i$ th residue, $r_i$ .

In the improper case, discussed in the next section, we additionally obtain an FIR part in the z transform to be inverted:

$$F(z) \eqsp f_0 + f_1z^{-1}+ f_2z^{-2}+ \cdots + f_K z^{-K} \;\longleftrightarrow\; [f_0,f_1,\ldots,f_K,0,0,\ldots].$$

The FIR part (a finite-order polynomial in $z^{-1}$ ) is also easily inverted by inspection.

The case of repeated poles is addressed in §6.8.5 below.