 C/C++ Vocal Tract Class
C/C++ Vocal Tract Class
 Digital Waveguide Modeling of the Vocal Tract
Digital Waveguide Modeling of the Vocal Tract
 Digital Waveguide Modeling of the Vocal Tract
Digital Waveguide Modeling of the Vocal Tract
An excellent derivation of the acoustic wave equation in a tube may be found in
[Cook 1990]. The main points are summarized here:
We require the formulae for point-wise conservation of momentum and mass within
the tube:
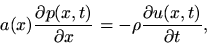 |
(1) |
and
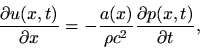 |
(2) |
where 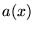 is the cross-sectional area of the tube at point
is the cross-sectional area of the tube at point 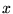 (in square
meters),
(in square
meters), 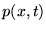 is the longitudinal pressure (in Newtons per square meter),
is the longitudinal pressure (in Newtons per square meter),
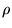 is the density of the fluid in the tube (in kilograms per cubic meter),
is the density of the fluid in the tube (in kilograms per cubic meter),
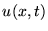 is the volume velocity of the fluid in the tube (in cubic meters
per second), and
is the volume velocity of the fluid in the tube (in cubic meters
per second), and 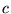 is the speed of sound in the fluid.
is the speed of sound in the fluid.
If 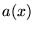 is assumed to be a constant,
is assumed to be a constant, 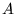 , then combining the two equations
yields
, then combining the two equations
yields
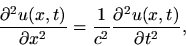 |
(3) |
or, for pressure,
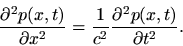 |
(4) |
These may each be recognized as dual forms of the homogeneous wave equation, the
solution of which allows for arbitrary left- and right-going traveling wave
components (these will be hereafter referred to as 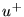 and
and 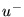 for
volume velocity, and
for
volume velocity, and 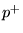 and
and 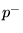 for pressure). The general solutions
to Eq. (3) and Eq. (4) are given by:
for pressure). The general solutions
to Eq. (3) and Eq. (4) are given by:
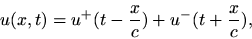 |
(5) |
and
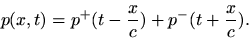 |
(6) |
Since the forward- and reverse-traveling wave components each satisfy the wave
equation separately (this can be shown by direct substitution),
Eq. (1) yields
and similarly, for the left-traveling wave component,
Define the characteristic impedance of the tube as
Consider a pair of tubes (with characteristic impedances 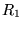 and
and 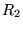 ) in
cascade. The scattering relation for the junction between these tubes may be
derived as follows:
) in
cascade. The scattering relation for the junction between these tubes may be
derived as follows:
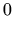 |
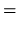 |
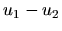 |
(16) |
| |
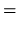 |
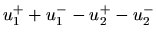 |
(17) |
| |
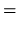 |
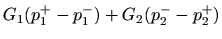 |
(18) |
| |
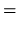 |
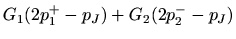 |
(19) |
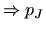 |
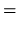 |
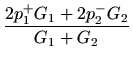 |
(20) |
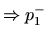 |
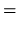 |
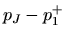 |
(21) |
| |
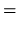 |
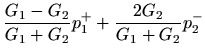 |
(22) |
| |
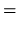 |
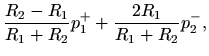 |
(23) |
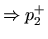 |
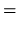 |
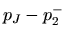 |
(24) |
| |
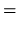 |
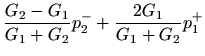 |
(25) |
| |
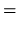 |
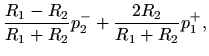 |
(26) |
where 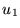 and
and 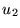 are the volume velocities in the two tubes at the
junction,
are the volume velocities in the two tubes at the
junction, 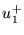 and
and 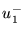 are the forward- and reverse-traveling volume
velocity wave components in tube 1 at the junction,
are the forward- and reverse-traveling volume
velocity wave components in tube 1 at the junction, 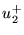 and
and 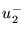 are
the forward- and reverse-traveling volume velocity wave components in tube 2 at
the junction,
are
the forward- and reverse-traveling volume velocity wave components in tube 2 at
the junction, 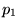 and
and 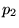 are the pressures in the two tubes at the
junction,
are the pressures in the two tubes at the
junction, 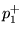 and
and 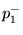 are the forward- and reverse-traveling
pressure wave components in tube 1 at the junction,
are the forward- and reverse-traveling
pressure wave components in tube 1 at the junction, 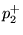 and
and 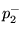 are
the forward- and reverse-traveling pressure wave components in tube 2 at the
junction,
are
the forward- and reverse-traveling pressure wave components in tube 2 at the
junction, 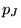 is the junction pressure (must be identical to
is the junction pressure (must be identical to 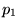 and
and 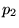 to avoid a pressure gradient across a zero-width (and hence, zero-mass)
section), and
to avoid a pressure gradient across a zero-width (and hence, zero-mass)
section), and
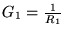 and
and
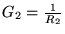 are the acoustic
conductances in the two tube sections. Note Eq. (16) expresses the
conservation of volume velocity, and Eq. (19) uses the aforementioned
continuity of pressure across the junction.
are the acoustic
conductances in the two tube sections. Note Eq. (16) expresses the
conservation of volume velocity, and Eq. (19) uses the aforementioned
continuity of pressure across the junction.
The following subsections deal with sample implementations of this vocal
synthesis technique.
 C/C++ Vocal Tract Class
C/C++ Vocal Tract Class
 Digital Waveguide Modeling of the Vocal Tract
Digital Waveguide Modeling of the Vocal Tract
 Digital Waveguide Modeling of the Vocal Tract
Digital Waveguide Modeling of the Vocal Tract
``Audio Speech Research Note'',
Ryan J. Cassidy,
published electronically by author, July 2003.
Download PDF version (audio_speech.pdf)
Download compressed PostScript version (audio_speech.ps.gz)
Copyright © 2003-11-28 by Ryan J. Cassidy.
Please email errata, comments, and suggestions to Ryan J. Cassidy <ryanc@ieee.org>
Stanford University
![]() is assumed to be a constant,
is assumed to be a constant, ![]() , then combining the two equations
yields
, then combining the two equations
yields
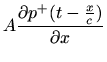
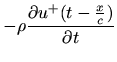
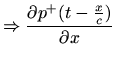
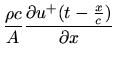
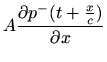
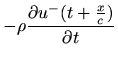
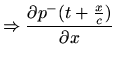
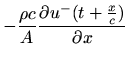
![]() and
and ![]() ) in
cascade. The scattering relation for the junction between these tubes may be
derived as follows:
) in
cascade. The scattering relation for the junction between these tubes may be
derived as follows: