Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
For definiteness, let's consider simulating the ideal vibrating
string, as shown in Fig. 1.
Figure 1:
The ideal vibrating string.
![\includegraphics[width=\textwidth]{eps/Fphysicalstring.eps}](img5.png) |
The wave equation for the ideal (lossless, linear, flexible)
vibrating string depicted in Fig. 1 is given by
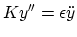 |
(1) |
where
and ``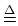 '' means ``is defined as.'' The wave equation is
derived, e.g., in [19].
'' means ``is defined as.'' The wave equation is
derived, e.g., in [19].
Subsections
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download wgfdtd.pdf
![\includegraphics[width=\textwidth]{eps/Fphysicalstring.eps}](img5.png)
