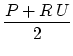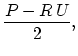WAVE DIGITAL MODELLING

Wave digital filter (WDF) techniques are used for digital simulation of analog networks [1, 2]. The resulting digital networks are called wave digital filters. The classical analogy between electric and acoustic systems allows application of similar techniques for the discretisation of lumped elements in an acoustic model. WDF techniques are similar to digital waveguide modelling (DWM) techniques in the sense that they both digitise continuous-time models using wave variables. A combined approach (``wave digital modelling'') is possible in which lumped elements are modelled using WDF techniques and distributed elements are modelled using DWM techniques. For example, in [6], such an approach has been taken for digital simulation of force interaction between hammer and string in a piano. In the current context of modelling acoustic wind instruments, the instantaneous acoustic variables are pressure (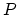$P$) and volume flow (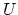$U$). We define the decompostion of these into wave variables as:

$$P^{+} = \frac{P + R \, U}{2}$$

$$\hfill \nopagebreak[4]$$ (1)

$$\nopagebreak[4] P^{-} = \frac{P - R \, U}{2}, \hfill$$

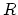where $R$ is the port-resistance. In the case of a distributed acoustic element, the wave variables correspond to pressure-waves travelling through a certain medium. The port-resistance then equals the reference impedance that characterises the medium (as in DWM). In the lumped case, the waves may only be understood to be travelling instantaneously [6]. From an acoustical point of view, the port-resistance may then be considered arbitrary. Similar to the derivation of WDFs (as described in [1, 2]), this freedom of choice can be used to avoid delay-free loops in the final discrete-time modelling structure.