Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Suppose a guitar bridge couples an ideal vibrating string to a single
resonance, as depicted schematically in Fig.9.5. This
is often an accurate model of an acoustic bridge impedance in a narrow
frequency range, especially at low frequencies where the resonances
are well separated. Then, as developed in Chapter 7, the
driving-point impedance seen by the string at the bridge is
That is, the driving-point impedance is the series combination of a
mass 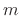 , spring
, spring 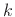 , and dashpot
, and dashpot 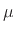 (§7.2). More
general bridge impedances can be modeled as a sum of such terms.
Since the bridge is passive,
(§7.2). More
general bridge impedances can be modeled as a sum of such terms.
Since the bridge is passive, 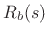 is positive real
(§C.11.2).
is positive real
(§C.11.2).
Figure 9.5:
Ideal vibrating string
terminated by a second-order driving-point impedance consisting of a
mass 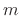 , spring
, spring 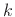 , and dashpot
, and dashpot 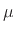 .
.
![\includegraphics[width=\twidth]{eps/f_yielding_term}](img2009.png) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![\includegraphics[width=\twidth]{eps/f_yielding_term}](img2009.png)