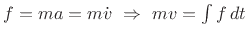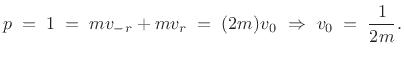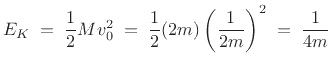Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
First, consider
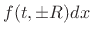 . That is, we apply an
upward unit-force impulse at time 0 in the middle of the rod. The
total momentum delivered in the neighborhood of
. That is, we apply an
upward unit-force impulse at time 0 in the middle of the rod. The
total momentum delivered in the neighborhood of 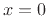 and
and 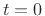 is
obtained by integrating the applied force density with respect to time
and position:
is
obtained by integrating the applied force density with respect to time
and position:
This unit momentum is transferred to the two masses 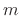 . By symmetry,
we have
. By symmetry,
we have
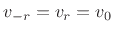 . We can also refer to
. We can also refer to 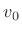 as the
velocity of the center of mass, again obvious by symmetry.
Continuing to refer to Fig.B.5, we have
as the
velocity of the center of mass, again obvious by symmetry.
Continuing to refer to Fig.B.5, we have
Thus, after time zero, each mass is traveling upward at speed
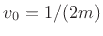 , and there is no rotation about the center of mass at
, and there is no rotation about the center of mass at
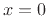 .
.
The kinetic energy of the system after time zero is
Note that we can also compute 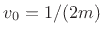 in terms of the total mass
in terms of the total mass 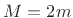 and the velocity of the center of mass
and the velocity of the center of mass
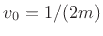 :
:
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() . That is, we apply an
upward unit-force impulse at time 0 in the middle of the rod. The
total momentum delivered in the neighborhood of
. That is, we apply an
upward unit-force impulse at time 0 in the middle of the rod. The
total momentum delivered in the neighborhood of ![]() and
and ![]() is
obtained by integrating the applied force density with respect to time
and position:
is
obtained by integrating the applied force density with respect to time
and position: