Next |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The transfer function of a normalized second-order lowpass can be written as
where the normalization maps the desired -3dB frequency 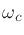 to 1, i.e.,
to 1, i.e.,
and the ``quality factor'' 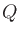 is defined as
is defined as
where 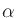 is a convenient definition for bandwidth in
radians per second, given by minus the real part of the
complex-conjugate pole locations
is a convenient definition for bandwidth in
radians per second, given by minus the real part of the
complex-conjugate pole locations 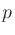 and
and 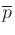 in the
in the 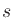 plane:1
plane:1
Here we assume
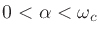 , so that the poles have nonzero imaginary parts.
, so that the poles have nonzero imaginary parts.
A second-order Butterworth lowpass filter is obtained for
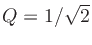 . Larger
. Larger 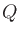 values give the ``corner resonance''
effect often used in music synthesizers.
values give the ``corner resonance''
effect often used in music synthesizers.
Next |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download svf.pdf
[Comment on this page via email]


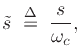
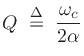
![]() . Larger
. Larger ![]() values give the ``corner resonance''
effect often used in music synthesizers.
values give the ``corner resonance''
effect often used in music synthesizers.