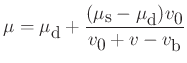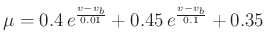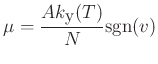Results

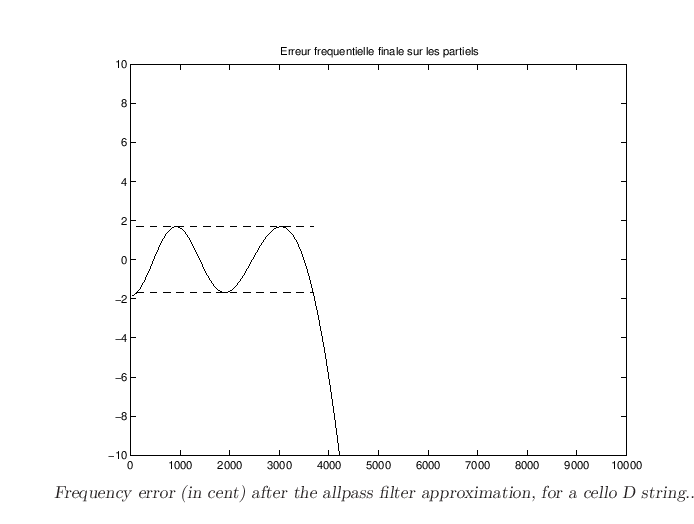
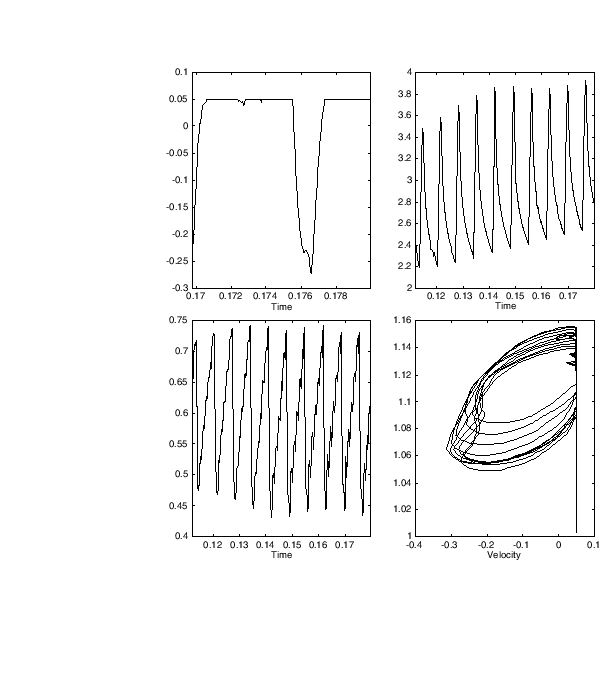
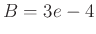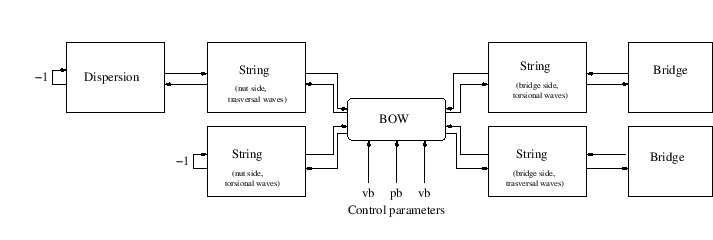
The figure below shows the results given by the algorithm, for a cello string (147 Hz) with $B=3e-4$ .

The friction models used in these simulations are:

• an hyperbola
  $$\mu=\mu_{\hbox{\small d}}+\frac{(\mu_{\hbox{\small s}}-\mu_{\hbox{\small d}}) v_{\hbox{\small0}}}{v_{\hbox{\small0}}+v-v_{\hbox{\small b}}}$$
  $\mu_{\hbox{\small d}}=0.3$ , $\mu_{\hbox{\small s}}=0.8$ .

  a sum of decaying exponentials:

  $$\mu=0.4 \, e^{\frac{v-v_{b}}{0.01}}+0.45 \, e^{\frac{v-v_{b}}{0.1}} +0.35$$

• a plastic model recently proposed by Jim Woodhouse, who discovered that friction does not depend only on the relative velocity between the bow and the string.

$$\mu=\frac{A k_{\hbox{\small y}}(T)}{N} \hbox{sgn}(v)$$

where

$$\begin{eqnarray*} A&=&\hbox{contact area between the bow and the string}\\ N&=&\hbox{normal load}\\ k_{\hbox{\small y}}(T) &=&\hbox{ shear yield stress as a function of the bow-string contact temperature $T$.} \end{eqnarray*}$$

• In the plastic model the key state variable governing the friction force is the temperature of the contact region.

• The notion of coefficient of friction is kept, but instead of depending on sliding speed it depends on contact temperature.

• The contact temperature, in turn, depends on the sliding velocity (recent history).