
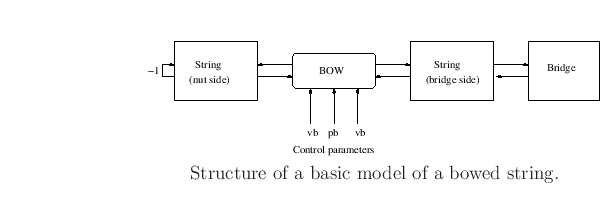
This model supposes that the bow is applied to a single point ![]() in
the string. When
in
the string. When ![]() , bow and string stick together, otherwise
they are sliding.
, bow and string stick together, otherwise
they are sliding.
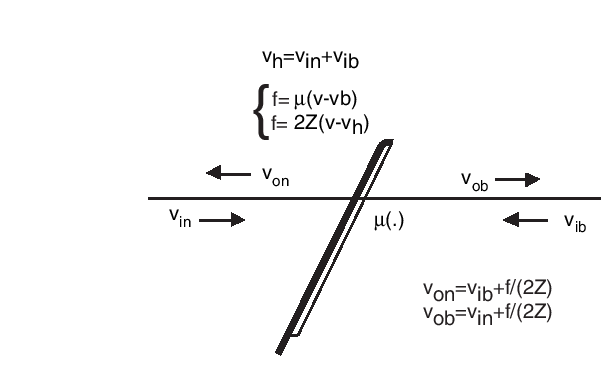
The contribution of the reflected waves ![]() and
and ![]() are
summed at the contact point:
are
summed at the contact point:
Bow string interaction is represented by the following relations:

Once this coupling has been solved, the new outgoing waves ![]() and
and ![]() are calculated by the following equations:
are calculated by the following equations:
