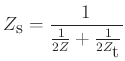Torsional waves can be modeled as an additional couple of waveguides
whose speed is about ![]() times the transverse wave speed.
times the transverse wave speed.
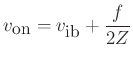
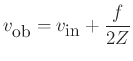
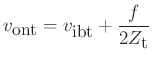

where ![]() applied force
applied force
![]() string transverse wave impedance
string transverse wave impedance
![]() string torsional wave impedance,
string torsional wave impedance,
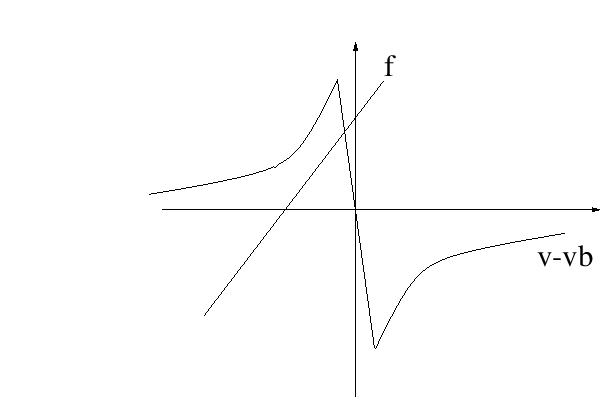
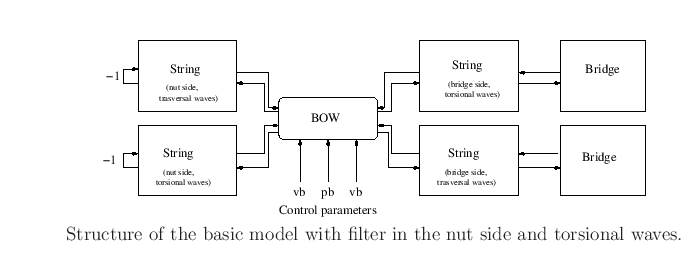
Torsional waves facilitate the establishment of Helmholtz motion
because they are more damped than the transversal waves.
Their contribution at the bow point can be modeled in two ways: