It's already been mentioned that the rectilinear coordinates of a complex
number ![]() in the complex plane are called the real part and
imaginary part, respectively.
in the complex plane are called the real part and
imaginary part, respectively.
We also have special notation and various names for the polar
coordinates
![]() of a complex number
of a complex number ![]() :
:
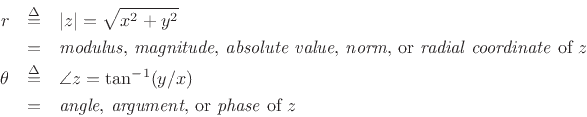
The complex conjugate of ![]() is denoted
is denoted
![]() (or
(or ![]() ) and is defined by
) and is defined by
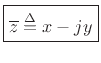
where, of course,
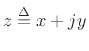 .
.
In general, you can always obtain the complex conjugate of any expression
by simply replacing ![]() with
with ![]() . In the complex plane, this is a vertical flip about the real axis; i.e., complex conjugation
replaces each point in the complex plane by its mirror image on the
other side of the
. In the complex plane, this is a vertical flip about the real axis; i.e., complex conjugation
replaces each point in the complex plane by its mirror image on the
other side of the ![]() axis.
axis.