Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Fourier Transform (FT) and Inverse
The Fourier transform of a signal
 ,
,
 , is defined as
, is defined as
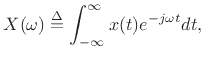 |
(B.1) |
and its inverse is given by
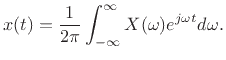 |
(B.2) |
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() ,
,
![]() , is defined as
, is defined as