Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Euler's identity (or ``theorem'' or ``formula'') is
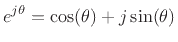
(Euler's Identity)
To ``prove'' this, we will first define what we mean by
``
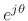 ''. (The right-hand side,
''. (The right-hand side,
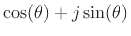 , is assumed to be understood.) Since
, is assumed to be understood.) Since 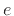 is just a
particular real number, we only really have to explain what we mean by
imaginary exponents. (We'll also see where
is just a
particular real number, we only really have to explain what we mean by
imaginary exponents. (We'll also see where 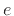 comes from in the
process.) Imaginary exponents will be obtained as a generalization of
real exponents. Therefore, our first task is to define exactly what
we mean by
comes from in the
process.) Imaginary exponents will be obtained as a generalization of
real exponents. Therefore, our first task is to define exactly what
we mean by 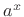 , where
, where 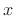 is any real number, and
is any real number, and 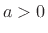 is any
positive real number.
is any
positive real number.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]