Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
In summary, we have characterized the mass on the string in terms of
its reflectance and transmittance from either string. For force
waves, we have outgoing waves given by
or
in terms of the incoming waves 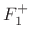 and
and 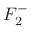 , the force
reflectance
, the force
reflectance
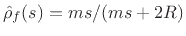 , and the force transmittance
, and the force transmittance
 . We may say that the mass
creates a dynamic scattering junction on the string. (If there
were no dependency on
. We may say that the mass
creates a dynamic scattering junction on the string. (If there
were no dependency on 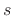 , such as when a dashpot is affixed to the
string, we would simply call it a scattering junction.)
, such as when a dashpot is affixed to the
string, we would simply call it a scattering junction.)
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![\begin{eqnarray*}
F^{-}_1(s) &=& \hat{\rho}_f(s) F^{+}_1(s) + \hat{\tau}_f(s) F^{-}_2(s)\\ [5pt]
F^{+}_2(s) &=& \hat{\tau}_f(s) F^{+}_1(s) + \hat{\rho}_f(s) F^{-}_2(s)
\end{eqnarray*}](img2157.png)
![\begin{eqnarray*}
F^{-}_1(s) &=& \hat{\rho}_f(s) F^{+}_1(s) + \hat{\tau}_f(s) F^{-}_2(s)\\ [5pt]
F^{+}_2(s) &=& \hat{\tau}_f(s) F^{+}_1(s) + \hat{\rho}_f(s) F^{-}_2(s)
\end{eqnarray*}](img2157.png)
![$\displaystyle \left[\begin{array}{c} F^{+}_2 \\ [2pt] F^{-}_1 \end{array}\right] \eqsp \left[\begin{array}{cc} \hat{\tau}_f(s) & \hat{\rho}_f(s) \\ [2pt] \hat{\rho}_f(s) & \hat{\tau}_f(s) \end{array}\right] \left[\begin{array}{c} F^{+}_1 \\ [2pt] F^{-}_2 \end{array}\right]
$](img2158.png)