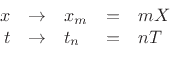Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Finite-Difference Schemes (FDSs) aim to solve differential
equations by means of finite differences. For example, as discussed
in §C.2, if  denotes the displacement in meters of a vibrating
string at time
denotes the displacement in meters of a vibrating
string at time 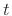 seconds and position
seconds and position 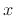 meters, we may approximate
the first- and second-order partial derivatives by
meters, we may approximate
the first- and second-order partial derivatives by
where 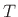 denotes the time sampling interval and
denotes the time sampling interval and  denotes the
spatial sampling interval. Other types of finite-difference schemes
were derived in Chapter 7 (§7.3.1), including a look at
frequency-domain properties. These finite-difference approximations
to the partial derivatives may be used to compute solutions of
differential equations on a discrete grid:
denotes the
spatial sampling interval. Other types of finite-difference schemes
were derived in Chapter 7 (§7.3.1), including a look at
frequency-domain properties. These finite-difference approximations
to the partial derivatives may be used to compute solutions of
differential equations on a discrete grid:
Let us define an abbreviated notation for the grid variables
and consider the ideal string wave equation (cf, §C.1):
 |
(D.2) |
where 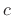 is a positive real constant (which turns out to be wave
propagation speed). Then, as derived in §C.2, setting
is a positive real constant (which turns out to be wave
propagation speed). Then, as derived in §C.2, setting
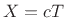 and substituting the finite-difference approximations into
the ideal wave equation leads to the relation
and substituting the finite-difference approximations into
the ideal wave equation leads to the relation
everywhere on the time-space grid (i.e., for all 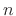 and
and 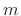 ). Solving
for
). Solving
for 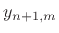 in terms of displacement samples at earlier times yields an
explicit finite-difference scheme
for string displacement:
in terms of displacement samples at earlier times yields an
explicit finite-difference scheme
for string displacement:
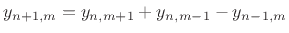 |
(D.3) |
The FDS is called explicit because it was possible to solve for
the state at time 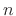 as a function of the state at earlier times (and
any other positions
as a function of the state at earlier times (and
any other positions 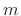 ). This allows it to be implemented as a time
recursion (or ``digital filter'') which computes a solution at time
). This allows it to be implemented as a time
recursion (or ``digital filter'') which computes a solution at time
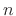 from solution samples at earlier times (and any spatial
positions). When an explicit FDS is not possible (e.g., a non-causal
filter is derived), the discretized differential equation is said to
define an implicit FDS. An implicit FDS
can often be converted to an explicit FDS by a rotation of coordinates
[55,484].
from solution samples at earlier times (and any spatial
positions). When an explicit FDS is not possible (e.g., a non-causal
filter is derived), the discretized differential equation is said to
define an implicit FDS. An implicit FDS
can often be converted to an explicit FDS by a rotation of coordinates
[55,484].
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() denotes the displacement in meters of a vibrating
string at time
denotes the displacement in meters of a vibrating
string at time ![]() seconds and position
seconds and position ![]() meters, we may approximate
the first- and second-order partial derivatives by
meters, we may approximate
the first- and second-order partial derivatives by