Euler's Equations for Rotations in the Body-Fixed Frame

Suppose now that the body-fixed frame is rotating in the space-fixed frame with angular velocity $\underline {\omega }$ . Then the total torque on the rigid body becomes [272]

$$\underline{\tau}\eqsp \dot{\underline{L}} + \underline{\omega}\times \underline{L}. \protect$$ (B.30)

Similarly, the total external forces on the center of mass become

$$\underline{f}\eqsp \dot{\underline{p}} + \underline{\omega}\times\underline{p}.$$

If the body-fixed frame is aligned with the principal axes of rotation (§B.4.16), then the mass moment of inertia tensor is diagonal, say $\mathbf{I}=$diag$(I_1,I_2,I_3)$ . In this frame, the angular momentum is simply

$$\underline{L}\eqsp \left[\begin{array}{c} I_1\omega_1 \\ [2pt] I_2\omega_2 \\ [2pt] I_3\omega_3\end{array}\right]$$

so that the term $\underline{\omega}\times\underline{L}$ becomes (cf. Eq.(B.15))

$$\begin{eqnarray*} \underline{\omega}\times\underline{L}&\!=\!& \left\vert \begin{array}{ccc} \underline{e}_1 & \underline{e}_2 & \underline{e}_3\\ [2pt] \underline{\omega}_1 & \underline{\omega}_2 & \underline{\omega}_3\\ [2pt] I_1\omega_1 & I_2\omega_2 & I_3\omega_3 \end{array}\right\vert\\ [5pt] &\!=\!& \mbox{\small$(\underline{\omega}_2 I_3\omega_3 - I_2\omega_2 \underline{\omega}_3)\underline{e}_1 + (\underline{\omega}_3I_1\omega_1 - I_3\omega_3\underline{\omega}_1) \underline{e}_2 + (\underline{\omega}_1I_2\omega_2- I_1\omega_1\underline{\omega}_2) \underline{e}_3$}\\ [5pt] &\!=\!& (I_3-I_2)\omega_2\omega_3\,\underline{e}_1 + (I_1-I_3)\omega_3\omega_1\,\underline{e}_2 + (I_2-I_1)\omega_1\omega_2\,\underline{e}_3. \end{eqnarray*}$$

Substituting this result into Eq.(B.30), we obtain the following equations of angular motion for an object rotating in the body-fixed frame defined by its three principal axes of rotation:

$$\begin{eqnarray*} \tau_1 &=& I_1 \dot{\omega}_1 + (I_3-I_2)\omega_2\omega_3\\ \tau_2 &=& I_2 \dot{\omega}_2 + (I_1-I_3)\omega_3\omega_1\\ \tau_3 &=& I_3 \dot{\omega}_3 + (I_2-I_1)\omega_1\omega_2 \end{eqnarray*}$$

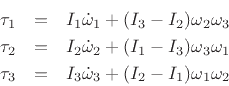
These are call Euler's equations:^B.29Since these equations are in the body-fixed frame, $I_i$ is the mass moment of inertia about principal axis $i$ , and $\omega_i$ is the angular velocity about principal axis $i$ .