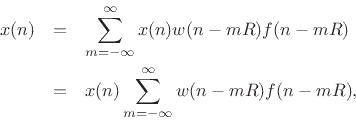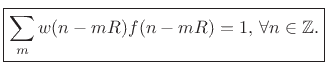WOLA Processing Steps

The sequence of operations in a WOLA processor can be expressed as follows:

1. Extract the 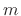$m$ th windowed frame of data 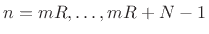$x_m(n)=x(n)w(n-mR)$ , $n=mR,\ldots,mR+N-1$ (assuming a length 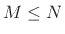$M\leq N$ causal window 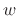$w$ and hop size $R$ ).

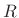2. Take an FFT of the 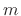$m$ th frame translated to time zero,
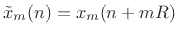   ${\tilde x}_m(n)=x_m(n+mR)$ , to produce the 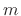$m$ th spectral frame
   ${\tilde X}_m(\omega_k)$ , $k=0,\ldots,N-1$ .

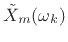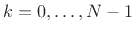3. Process 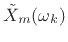${\tilde X}_m(\omega_k)$ as desired to produce ${\tilde Y}_m(\omega_k)$ .

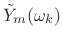4. Inverse FFT 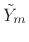${\tilde Y}_m$ to produce ${\tilde y}_m(n)$ , $n=0,\ldots,N-1$ .

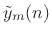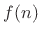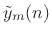5. Apply a synthesis window $f(n)$ to ${\tilde y}_m(n)$ to yield a weighted output frame ${\tilde y}^f_m(n) = {\tilde y}_m(n)f(n)$ , $n=0,\ldots,N-1$ .

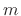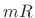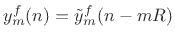6. Translate the $m$ th output frame to time $mR$ as $y^f_m(n) = {\tilde y}^f_m(n-mR)$ and add to the accumulated output signal $y(n)$ .

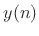(The overlap-add method discussed previously is obtained from the above procedure by deleting step 5.)

To obtain perfect reconstruction in the absence of spectral modifications, we require

$$\begin{eqnarray*} x(n) &=& \sum_{m=-\infty}^{\infty} x(n) w(n-mR)f(n-mR) \\ &=& x(n) \sum_{m=-\infty}^{\infty} w(n-mR)f(n-mR), \end{eqnarray*}$$

which is true if and only if

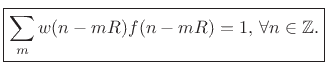$$\zbox {\sum_m w(n-mR)f(n-mR) = 1, \,\forall n\in\mathbb{Z}.}$$ (9.44)