Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
In view of Chapter 8, a natural implementation of TSM based on the
STFT is as follows:
- Perform a short-time Fourier transform (STFT) using hop size
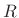 . Denote the STFT at frame
. Denote the STFT at frame 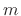 and bin
and bin 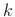 by
by
 , and
denote the result of TSM processing by
, and
denote the result of TSM processing by
 .
.
- To perform TSM by the factor
 , advance the ``frame
pointer''
, advance the ``frame
pointer'' 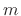 by
by  during resynthesis instead of the usual
during resynthesis instead of the usual
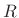 samples.
samples.
For example, if 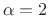 (
( slow-down), the first STFT frame
slow-down), the first STFT frame
 is processed normally, so that
is processed normally, so that  . However, the
second output frame
. However, the
second output frame  corresponds to a time
corresponds to a time  , half way
between the first two frames. This output frame may be created by
interpolating (across time) the STFT magnitude magnitude
spectra of the first. For example, using simple linear interpolation
gives
, half way
between the first two frames. This output frame may be created by
interpolating (across time) the STFT magnitude magnitude
spectra of the first. For example, using simple linear interpolation
gives
 |
(11.23) |
where the phase
 is chosen to preserve continuity
and/or the amplitude envelope from frame to frame under the
overlap-add (more on this below). Generalizing to arbitrary TSM
factors
is chosen to preserve continuity
and/or the amplitude envelope from frame to frame under the
overlap-add (more on this below). Generalizing to arbitrary TSM
factors  , we obtain
, we obtain
![$\displaystyle Y_{m}(\omega_k) \eqsp \left[ (1-\eta)\, \vert X_{\left\lfloor m\right\rfloor }(\omega_k)\vert + \eta\,\vert X_{\left\lceil m\right\rceil }(\omega_k)\vert \right]\, e^{j\theta_m(\omega_k)}$](img1854.png) |
(11.24) |
where
 , and
, and 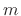 is advanced by
is advanced by
 each frame-step.
each frame-step.
In general, TSM methods based on STFT modification are classified as
``vocoder'' type methods (§G.5). Thus, the TSM
implementation outlined above may be termed a
weighted overlap-add (WOLA) phase-vocoder
method.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() (
(![]() slow-down), the first STFT frame
slow-down), the first STFT frame
![]() is processed normally, so that
is processed normally, so that ![]() . However, the
second output frame
. However, the
second output frame ![]() corresponds to a time
corresponds to a time ![]() , half way
between the first two frames. This output frame may be created by
interpolating (across time) the STFT magnitude magnitude
spectra of the first. For example, using simple linear interpolation
gives
, half way
between the first two frames. This output frame may be created by
interpolating (across time) the STFT magnitude magnitude
spectra of the first. For example, using simple linear interpolation
gives
