Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Practical Computation of the STFT
While the definition of the STFT in (7.1) is useful for
theoretical work, it is not really a specification of a practical
STFT. In practice, the STFT is computed as a succession of FFTs of
windowed data frames, where the window ``slides'' or ``hops'' forward
through time. We now derive such an implementation of the STFT from
its mathematical definition.
The STFT in (7.1) can be rewritten, adding 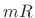 to
to 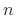 , as
, as
In this form, the data centered about time 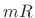 are translated to time
0, multiplied by the (let's assume zero-phase) window
are translated to time
0, multiplied by the (let's assume zero-phase) window 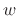 , and then
the DTFT is performed. Since the nonzero portion of the windowed data
is centered on time zero, the DTFT can be replaced by the DFT (or
FFT). This effectively samples the DTFT in frequency. This
sampling will not cause (time) aliasing if the number of samples
around the unit circle is greater than the width (in samples) of the
time interval including all nonzero datapoints. In other words,
sampling the frequency axis is information-preserving when the signal
is properly
time limited.8.3Let
, and then
the DTFT is performed. Since the nonzero portion of the windowed data
is centered on time zero, the DTFT can be replaced by the DFT (or
FFT). This effectively samples the DTFT in frequency. This
sampling will not cause (time) aliasing if the number of samples
around the unit circle is greater than the width (in samples) of the
time interval including all nonzero datapoints. In other words,
sampling the frequency axis is information-preserving when the signal
is properly
time limited.8.3Let  denote the window length (typically an
odd number) and
denote the window length (typically an
odd number) and 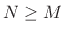 be the DFT length (typically a power of 2). Then
sampling (7.3) at
be the DFT length (typically a power of 2). Then
sampling (7.3) at
 ,
,
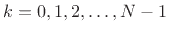 , and using the fact that the window
, and using the fact that the window 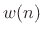 is
time-limited to less than
is
time-limited to less than  samples centered about time zero, yields
samples centered about time zero, yields
Since indexing in the DFT is modulo  , the sum over
, the sum over 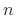 can be
``rotated'' to a sum from 0 to
can be
``rotated'' to a sum from 0 to  as is conventionally implemented
for the DFT. In practice, this means that the right half of the
windowed data frame goes at the beginning of the FFT input buffer, and
the left half of the windowed frame goes at the end, with zero-padding
in the middle (see Fig.2.6b on page
as is conventionally implemented
for the DFT. In practice, this means that the right half of the
windowed data frame goes at the beginning of the FFT input buffer, and
the left half of the windowed frame goes at the end, with zero-padding
in the middle (see Fig.2.6b on page ![[*]](../icons/crossref.png) for
an illustration).
for
an illustration).
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() to
to ![]() , as
, as