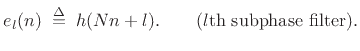Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
N-Channel
Polyphase Decomposition
Figure 11.9:
Schematic illustration of three interleaved polyphase signal components.
![\includegraphics[scale=0.8]{eps/polytime}](img1957.png) |
For the general case of arbitrary 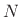 , the basic idea is to decompose
, the basic idea is to decompose
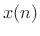 into its periodically interleaved subsequences, as indicated
schematically in Fig.11.9. The polyphase decomposition into
into its periodically interleaved subsequences, as indicated
schematically in Fig.11.9. The polyphase decomposition into
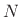 channels is given by
channels is given by
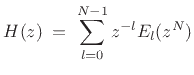 |
(12.11) |
where the subphase filters are defined by
 |
(12.12) |
with
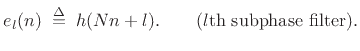 |
(12.13) |
The signal 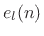 can be obtained by passing
can be obtained by passing 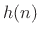 through an
advance of
through an
advance of 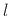 samples, followed by downsampling by the factor
samples, followed by downsampling by the factor 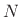 .
as shown in Fig.11.10.
.
as shown in Fig.11.10.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![\includegraphics[scale=0.8]{eps/polytime}](img1957.png)
![]() , the basic idea is to decompose
, the basic idea is to decompose
![]() into its periodically interleaved subsequences, as indicated
schematically in Fig.11.9. The polyphase decomposition into
into its periodically interleaved subsequences, as indicated
schematically in Fig.11.9. The polyphase decomposition into
![]() channels is given by
channels is given by