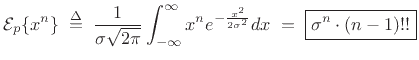Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Theorem:
The 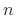 th central moment of the Gaussian pdf
th central moment of the Gaussian pdf 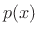 with mean
with mean  and variance
and variance 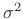 is given by
is given by
![$\displaystyle m_n \isdef {\cal E}_p\{(x-\mu)^n\} = \left\{\begin{array}{ll} (n-1)!!\cdot\sigma^n, & \hbox{$n$\ even} \\ [5pt] $0$, & \hbox{$n$\ odd} \\ \end{array} \right. \protect$](img2825.png) |
(D.44) |
where 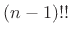 denotes the product of all odd integers up to and
including
denotes the product of all odd integers up to and
including 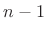 (see ``double-factorial notation'').
Thus, for example,
(see ``double-factorial notation'').
Thus, for example,
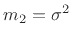 ,
,
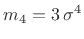 ,
,
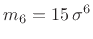 , and
, and
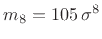 .
.
Proof:
The formula can be derived by successively differentiating the
moment-generating function
 with respect to
with respect to  and evaluating at
and evaluating at 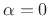 ,D.4 or by differentiating the
Gaussian integral
,D.4 or by differentiating the
Gaussian integral
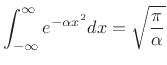 |
(D.45) |
successively with respect to  [203, p. 147-148]:
[203, p. 147-148]:
for
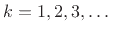 .
Setting
.
Setting
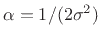 and
and  , and dividing both sides by
, and dividing both sides by
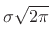 yields
yields
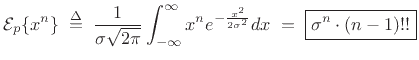 |
(D.46) |
for
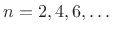 . Since the change of variable
. Since the change of variable
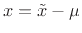 has no affect on the result,
(D.44) is also derived for
has no affect on the result,
(D.44) is also derived for 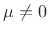 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() th central moment of the Gaussian pdf
th central moment of the Gaussian pdf ![]() with mean
with mean ![]() and variance
and variance ![]() is given by
is given by
![]() with respect to
with respect to ![]() and evaluating at
and evaluating at ![]() ,D.4 or by differentiating the
Gaussian integral
,D.4 or by differentiating the
Gaussian integral
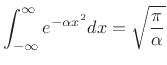
![\begin{eqnarray*}
\int_{-\infty}^\infty (-x^2) e^{-\alpha x^2} dx &=& \sqrt{\pi}(-1/2)\alpha^{-3/2}\\
\int_{-\infty}^\infty (-x^2)(-x^2) e^{-\alpha x^2} + dx &=& \sqrt{\pi}(-1/2)(-3/2)\alpha^{-5/2}\\
\vdots & & \vdots\\
\int_{-\infty}^\infty x^{2k} e^{-\alpha x^2} dx &=& \sqrt{\pi}\,[(2k-1)!!]\,2^{-k/2}\alpha^{-(k+1)/2}
\end{eqnarray*}](img2834.png)
![]() .
Setting
.
Setting
![]() and
and ![]() , and dividing both sides by
, and dividing both sides by
![]() yields
yields